SOLUTION

Given Data

Supply Voltage V = 220 V
Speed N₁ = 1000 RPM
Armature Resistance R_a = 0.25 Ω
Line Current I_L = 68A & 52.8A
Field current I_F = 2.2 A & 1.8 A
Speed N₂ = 1600 RPM

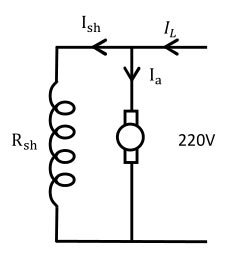
The Line current of DC shunt motor is the sum of Armature current and Shunt field current

I_L = I_a + I_sh

∴ I_a = I_L − I_sh

I_a1 = 68 − 2.2 = 65.8 A

From the voltage equation, the Back EMF will be

E_b1 = V − I_a1R_a

= 220 × 65.8 × 0.25

 E_b1 = 203.55

Similarly for the line current of 52.8 A and a field current of 1.8 A the armature current will be

I_a2 = 52.8 − 1.8 = 51 A

Hence E_b2 = V − I_a2R_a

= 220 × 51 × 0.25

 E_b2 = 207.25

Let the on load speed be N. As we know that back EMF of DC motor is directly proportional to the flux and speed.

E_b ∝ Nφ

$\begin{array}{l}\dfrac{{{E_{b1}}}}{{{E_{b2}}}} = \dfrac{{{N_1}}}{{{N_2}}} \times \dfrac{{{\Phi _1}}}{{{\Phi _2}}}\\\\\dfrac{{203.55}}{{207.25}} = \dfrac{{1000}}{{1600}} \times \dfrac{{{\Phi _1}}}{{{\Phi _2}}}\\\\\dfrac{{{\Phi _2}}}{{{\Phi _1}}} = 0.6364\\\\\therefore \% {\text{ Decrease = }}\dfrac{{{\Phi _1} – {\Phi _2}}}{{{\Phi _1}}} \times 100\\\\ = 1 – \dfrac{{{\Phi _2}}}{{{\Phi _1}}} = 1 – 0.6364\\\\ = 0.3636 \times 100 = 36.36\end{array}$