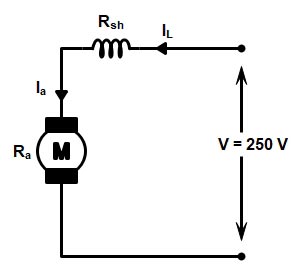
A 4 pole, 250 V, DC series motor has a wave-connected armature with 200 conductors. The flux per pole is 25 mWb when the motor is drawing 60 A from the supply. The armature resistance is 0.15 Ω while the series field winding resistance is 0.2 Ω. Calculate the speed under this condition.
Right Answer is:
1374 RPM
SOLUTION
Given Data
Supply Voltage V = 250 V
Number of Poles P = 4
Total number of armature conductors Z = 200
Number of parallel paths in the armature winding A = 2 (for wave winding number of parallel path is always 2)
Line current IL = 60 A
Armature current Ia = 60 A ( In DC series motor the line current is equal to the armature current i.e IL = Ia)
Flux Φ = 25 x 10-3
Armature Resistance Ra = 0.15Ω
Series Resistance Rse = 0.2Ω
The Back EMF of DC series Motor is given by
Eb = V − Ia(Ra + Rse)
= 250 − 60 (0.15 + 0.2)
= 250 − 21
Eb = 229
Back EMF in DC Motor Eb.
${E_b} = \dfrac{{P\Phi ZN}}{{60A}}$
Where
P – Number of poles of the machine
ϕ – Flux per pole in Weber.
Z – Total number of armature conductors.
N – Speed of armature in revolution per minute (r.p.m).
A – Number of parallel paths in the armature winding.
$\begin{array}{l}N = \dfrac{{{E_b} \times 60A}}{{P\Phi Z}}\\\\ = \dfrac{{229 \times 60 \times 2}}{{4 \times 25 \times {{10}^{ – 3}} \times 200}}\\\\N = 1374{\text{ R}}{\rm{.P}}{\rm{.M}}\end{array}$
