A 500 V shunt motor runs at its normal speed of 250 RPM when the armature current is 200 A. The resistance of armature is 0.12 Ω. Calculate the speed when resistance is inserted in the field reducing the shunt field to 80% of normal value and the armature current is 100A.
Right Answer is:
320 RPM
SOLUTION
Given that
Supply voltage Vs = 500 V
Speed N1 = 250 RPM
Armature current Ia1= 200 A
Armature Resistance R1 = 0.12Ω
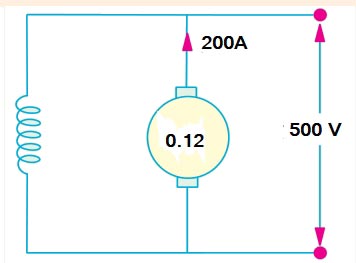
Back EMF of DC Motor is given as
Eb = V − IaRa
Eb = 500 − 200 × 0.12 = 478V
Now when the resistance is inserted in the field, Flux reduce to 80%
Flux Φ2 = 0.8Φ1
Armature current Ia2 = 100A
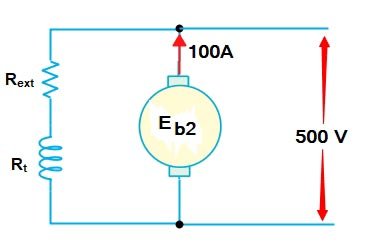
Back EMF
Eb = V − IaRa
Eb = 500 − 100 × 0.12 = 488V
As we Know that In DC motor the back EMF is directly proportional to the speed and flux.
E ∝ Nφ
$\begin{array}{l}\dfrac{{{E_{b2}}}}{{{E_{b1}}}} = \dfrac{{{N_2}}}{{{N_1}}} \times \dfrac{{{\Phi _2}}}{{{\Phi _1}}}\\\\{N_2} = {N_1} \times \dfrac{{{E_{b2}}}}{{{E_{b1}}}} \times \dfrac{{{\Phi _2}}}{{{\Phi _1}}}\\\\{N_2} = 250 \times \dfrac{{488}}{{476}} \times \left( {\dfrac{{{\Phi _1}}}{{0.8{\Phi _1}}}} \right)\\\\{N_2} = 320{\rm{ R}}{\text{.P}}{\rm{.M}}\end{array}$
