1. The system described by the equation y(n)=ay(n-1)+b x(n) is a recursive system.
A. True
B. False
2. To implement the linear time invariant recursive system described by the difference equation y(n)=\(-\sum_{k=1}^N a_k y(n-k)+\sum_{k=0}^M b_k x(n-k)\) in Direct form-I, how many number of delay elements and multipliers are required respectively?
A. M+N+1, M+N
B. M+N-1, M+N
C. M+N, M+N+1
D. None of the mentioned
3. Which of the following linear time invariant system is a purely recursive system?
A. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)
B. y(n) = \(\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)
C. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)-\sum_{k=0}^{M} b_k x(n-k)\)
D. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+b_0x(n)\)
4. Which of the following is the difference equation of a special case of FIR system?
A. y(n) = \(\sum_{k=0}^{M} b_k x(n-k)\)
B. y(n) = \(a_0y(n)-\sum_{k=1}^{N} a_k y(n-k)\)
C. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)\)
D. None of the mentioned
5. What is the system does the following directly from structure represent?
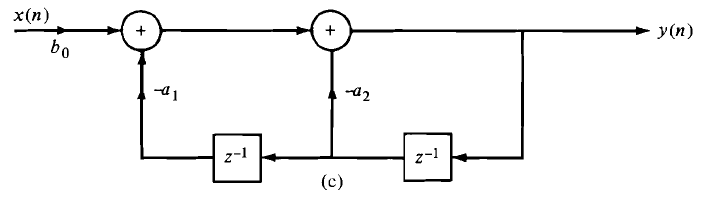
A. FIR system
B. Purely recursive system
C. General second-order system
D. None of the mentioned
6. What is the output of the system represented by the following direct form?
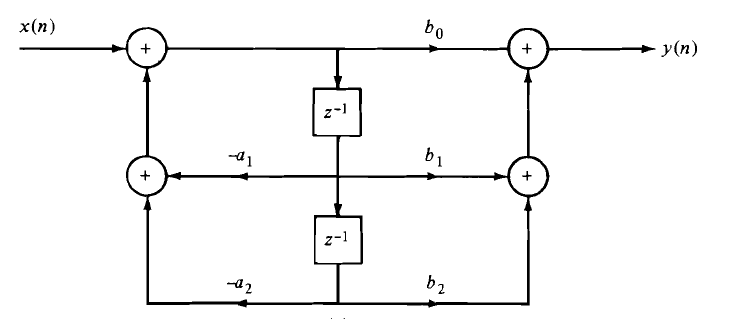
A. y(n)=-a1y(n-1)-a2y(n-2)- b0x(n)-b1x(n-1)-b2x(n-2)
B. y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)
C. y(n)=-a1y(n-1)-a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)
D. y(n)=a1y(n-1)+a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)
7. The system represented by the following direct form structure is:
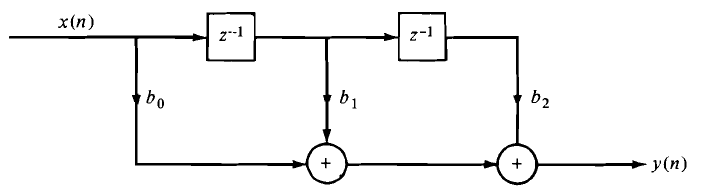
A. General second-order system
B. Purely recursive system
C. Partial recursive system
D. FIR system
8. An FIR system is also called as “recursive system”.
A. True
B. False
9. What is the form of the FIR system to compute the moving average of the signal x(n)?
A. y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n-k)\)
B. y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n+k)\)
C. y(n)=\(\frac{1}{M+1} \sum_{k=0}^{\infty} x(n-k)\)
D. None of the mentioned
10. Which of the following is a recursive form of a non-recursive system described by the equation y(n)=\(\frac{1}{M+1} \sum_{k=0}^Mx(n-k)\)?
A. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1-M)]
B. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1+M)]
C. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1+M)]
D. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1-M)]
