Discrete Time System Implementation MCQ Quiz – Objective Question with Answer for Discrete Time System Implementation

1. The system described by the equation y(n)=ay(n-1)+b x(n) is a recursive system.

A. True
B. False

Answer: A

Since the present output depends on the value of the previous output, the system is called a Recursive system.

2. To implement the linear time invariant recursive system described by the difference equation y(n)=\(-\sum_{k=1}^N a_k y(n-k)+\sum_{k=0}^M b_k x(n-k)\) in Direct form-I, how many number of delay elements and multipliers are required respectively?

A. M+N+1, M+N
B. M+N-1, M+N
C. M+N, M+N+1
D. None of the mentioned

Answer: C

From the given equation, there are M+N delays, so it requires M+N number of delay elements and it has to perform M+N+1 multiplications, so it requires many numbers of multipliers.

3. Which of the following linear time invariant system is a purely recursive system?

A. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)

B. y(n) = \(\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)

C. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)-\sum_{k=0}^{M} b_k x(n-k)\)

D. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+b_0x(n)\)

Answer: D

Since the output of the system depends only on the past values of output and the present value of the input, the system is called as “purely recursive” system.

4. Which of the following is the difference equation of a special case of FIR system?

A. y(n) = \(\sum_{k=0}^{M} b_k x(n-k)\)

B. y(n) = \(a_0y(n)-\sum_{k=1}^{N} a_k y(n-k)\)

C. y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)\)

D. None of the mentioned

Answer: A

If the coefficients of the past values of the output in the difference equation of the system, then the system is said to be an FIR system.

5. What is the system does the following directly from structure represent?

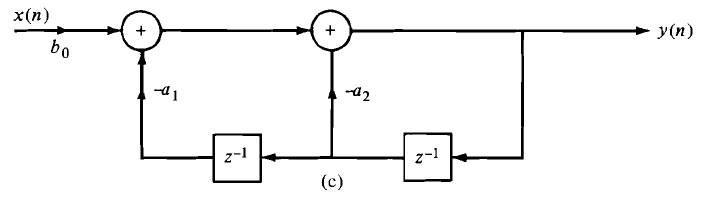
A. FIR system
B. Purely recursive system
C. General second-order system
D. None of the mentioned

Answer: B

Since the output of the system depends only on the present value of the input and the past values of the output, the system is a purely recursive system.

6. What is the output of the system represented by the following direct form?

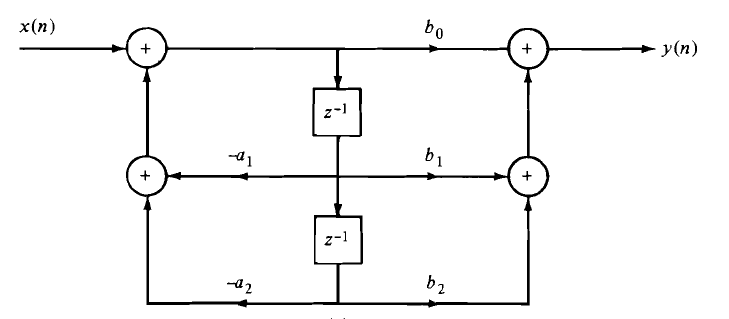
A. y(n)=-a1y(n-1)-a2y(n-2)- b0x(n)-b1x(n-1)-b2x(n-2)
B. y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)
C. y(n)=-a1y(n-1)-a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)
D. y(n)=a1y(n-1)+a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)

Answer: C

The equation of the difference equation of any system is defined as

y(n)=\(-\sum_{k=1}^Na_k y(n-k)+\sum_{k=0}^{M}b_k x(n-k)\)

In the given diagram, N=M=2

So, substitute the values of the N and M in the above equation.

We get, y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)+b1x(n-1)+b2x(n-2)

7. The system represented by the following direct form structure is:

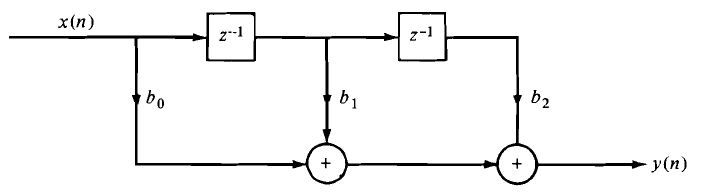
A. General second-order system
B. Purely recursive system
C. Partial recursive system
D. FIR system

Answer: D

The output of the system according to the direct form given is
y(n)= b0x(n)+b1x(n-1)+b2x(n-2)
Since the output of the system is purely dependent on the present and past values of the input, the system is called an FIR system.

8. An FIR system is also called as “recursive system”.

A. True
B. False

Answer: B

For a system to be recursive, the output of the system must be dependent only on the past values of the output. For an FIR system, the output of the system must be depending only on the present and past values of the input. So, the FIR system is not recursive.

9. What is the form of the FIR system to compute the moving average of the signal x(n)?

A. y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n-k)\)

B. y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n+k)\)

C. y(n)=\(\frac{1}{M+1} \sum_{k=0}^{\infty} x(n-k)\)

D. None of the mentioned

Answer: A

A normal FIR non-recursive system with the impulse response h(n)=\(\frac{1}{M+1}\) is the system that is used to compute the moving average of a signal x(n).

10. Which of the following is a recursive form of a non-recursive system described by the equation y(n)=\(\frac{1}{M+1} \sum_{k=0}^Mx(n-k)\)?

A. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1-M)]

B. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1+M)]

C. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1+M)]

D. y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1-M)]

Answer: D

The given system equation is

y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n-k)\)

It can be expressed as follows

\(y(n)=\frac{1}{M+1} \sum_{k=0}^M x(n-1-k)+\frac{1}{M+1}[x(n)-x(n-1-M)]\)

=\(y(n-1)+\frac{1}{M+1}[x(n)-x(n-1-M)]\)

Pages: 1 2 3

Related Posts