First & Second-Order High Pass Butterworth Filter and Higher Order Filters MCQ

1. How are the higher-order filters formed?

A. By increasing resistors and capacitors in low pass filter
B. By decreasing resistors and capacitors in low pass filter
C. By interchanging resistors and capacitors in low pass filter
D. All of the mentioned

Answer: C

High pass filters are often formed by interchanging frequency determining resistors and capacitors in low pass filters. For example, a first-order high pass filter is formed from a first-order low pass filter by interchanging components Rand C.

2. In a first-order high pass filter, frequencies higher than low cut-off frequencies are called
A. Stopband frequency
B. Passband frequency
C. Centre band frequency
D. None of the mentioned

Answer: B

The low cut-off frequency, f_L is 0.707 times the passband gain voltage. Therefore, frequencies above f_L are passband frequencies.

3. Compute the voltage gain for the following circuit with an input frequency 1.5kHz.

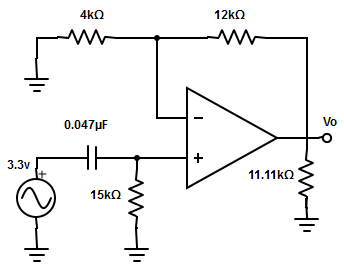
A. 4dB
B. 15dB
C. 6dB
D. 12dB

Answer: D

|V_O/V_in|= [A_F×(f/f_L)]/ [√1+(f/f_L)²]

= [4×(1.5kHz/225.86)] / √[1+(1.5kHz/225.86)²]

=26.56/6.716=3.955

=20log(3.955)=11.9.

|V_O/V_in|≅12 dB

A_F= 1+(R_F /R₁)= 1+(12kΩ/4kΩ) =4.

f_L= 1/(2πRC. = 1/2π×15kΩ×0.047µF

= 1/4.427×10^-3 =225.86Hz.

4. Determine the expression for the output voltage of the first-order high pass filter?

A. V_O = [1+(R_F /R₁)]× [(j2πfRC/(1+j2πfRC.] × V_in

B. V_O = [-(R_F /R₁)]× [(j2πfRC/(1+j2πfRC.] × V_in

C. V_O = {[1+(R_F /R₁)]× /[1+j2πfRC] }× V_in

D. None of the mentioned

Answer: A

The first-order high pass filter uses a non-inverting amplifier.

So, A_F= 1+(R_F /R₁), and the output voltage,

V_O = [1+(R_F /R₁)]× [(j2πfRC/(1+j2πfRC.]× V_in.

5. The internal resistor of the second-order high pass filter is equal to 10kΩ. Find the value of the feedback resistor?

A. 6.9kΩ
B. 5.86kΩ
C. 10kΩ
D. 12.56kΩ

Answer: B
Pass band gain for second order butterworth response,

A_F =1.586.

=> A_F= [1+(R_F/R₁)]

=> R_F= (A_F-1)×R₁

=(1.586-1)×10kΩ

=5860 =5.86kΩ.

6. Consider the following circuit and calculate the low cut-off frequency value?

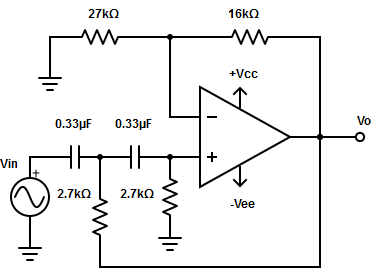
A. 178.7Hz
B. 89.3Hz
C. 127.65Hz
D. 255.38Hz

Answer: A

The low cut-off frequency for the given filter is

f_L =1/√[2π√(R₂×R₃×C₂×C₃)] =178.7Hz.

7. Determine voltage gain of second-order high pass Butterworth filter.
Specifications R₃ =R₂=33Ω, f=250hz and f_L=1khz.

A. -11.78dB
B. -26.51dB
C. -44.19dB
D. None of the mentioned

Answer: C

Since R₃ =R₂

=> C₂ = 1/(2π ×f_L×R₂)

= 1/(2π ×1kHz×33Ω)

=> C₃ =C₂= 4.82µF.

Voltage gain of filter |V_O/V_in|

=A_F / [√ 1+(f_L/f)⁴]

= 1.586/[1+(1kHz/250kz)⁴]

=1.586/252=6.17×10^-3

=20log(6.17×10^-3)= -44.19dB.

8. From the given specifications, determine the value of voltage gain magnitude of the first order and second-order high pass Butterworth filter?

Pass band voltage gain=2;
Low cut-off frequency= 1kHz;
Input frequency=500Hz.

A. First order high pass filter =-4.22dB , Second order high pass filter=-0.011dB

B. First order high pass filter =-0.9688dB , Second order high pass filter=-6.28dB

C. First order high pass filter =-11.3194dB , Second order high pass filter=-9.3257dB

D. First order high pass filter =-7.511dB , Second order high pass filter=-5.8999dB

Answer: B

For first order high pass filter,

|V_O/V_in|=A_F ×(f/f_L) / [ √1+(f/f_L)²]

=(2×(500Hz/1kHz)) /√[1+(500Hz/1kHz)²]

=> |V_O/V_in| = 1/1.118= 0.8944

=20log(0.8944) =-0.9686dB.

For second order high pass filter,

|V_O/V_in|=A_F / [ √ 1 +(f_L/f)⁴]

=2/√[1+ (1kHz/500Hz)²]

=>|V_O/V_in|=2/4.123

=0.4851 = 20log(0.4851) = -6.28dB.

9. How are the higher-order filters formed?

A. Using the first-order filter
B. Using second-order filter
C. Connecting first and second-order filters in series
D. Connecting first and second-order filters in parallel

Answer: C

Higher filters are formed by using the first and second-order filters. For example, a third-order low pass filter is formed by cascading first and second-order low pass filters.

10. State the disadvantage of using higher-order filters?

A. Complexity
B. Requires more space
C. Expensive
D. All of the mentioned

Answer: D

Although a higher-order filter than necessary gives a better stop band response, the higher-order type is more complex, occupies more space, and is more expensive.

Pages: 1 2

Related Posts