Kirchhoff’s Voltage Law (KVL) MCQ
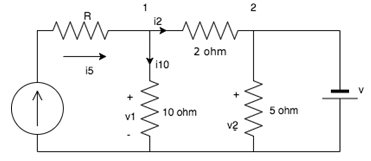
1. Find the value of v if v1 = 20V and the value of the current source are 6A.
A. 10V
Show Explanation
Answer: B. 12 V
The current through the 10 ohm resistor = v1/10 = 2A.
Applying KCL at node 1:
i5 = i10+i2. i2 = 6-2 = 4A.
Thus the drop in the 2 ohm resistor = 4 × 2 = 8V.
v1 = 20V;
hence v2 = 20-v across 2 ohm resistor = 20-8 = 12V
v2 = v s
Since they are connected in parallel.
v = 12V.
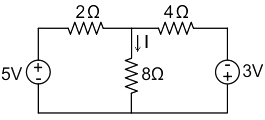
2. In the circuit shown in the figure, find the current flowing through the 8 Ω resistance.
0.25 A
0.50 A
0.75 A
0.10 A
Show Explanation
Answer.1. 0.25A
Let voltage across the 8 Ω resistance is ‘V’ volt.
∴ Current across the 8 Ω is given by
I = V/8
Now by applying KCL at the node we get
\({{V – 5} \over 2}+{{V +3} \over 4}+{{V } \over 8}=0\)
4V – 20 + 2V + 6 + V = 0
V = 14/7
Now current flowing through the 8 Ω resistance is
I = 2/8
I = 0.25 A
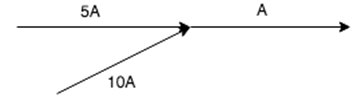
3. Calculate the current A by using Kirchhoff’s current law
A. 5A
Show Explanation
Answer: C
KCl states that the total current leaving the junction is equal to the current entering it. In this case, the current entering the junction is 5A+10A = 15A.
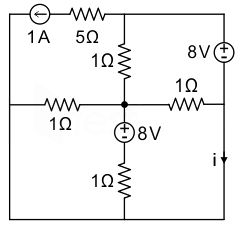
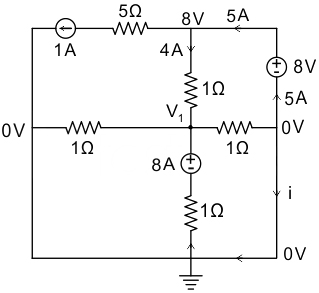
4. In the figure shown, the current 𝑖 (in ampere) is __________
-1 Amp
5 Amp
2 Amp
-2 Amp
Show Explanation
Answer.1. -1 Amp
Apply KCL at node V1 , we get:
\(\frac{{{{\rm{V}}_1} – 0}}{1} + \frac{{{{\rm{V}}_1} – 8}}{1} + \frac{{{{\rm{V}}_1} – 0}}{1} + \frac{{{{\rm{V}}_1} – 8}}{1} = 0\)
4V1 – 16 = 0
V1 = 4 V
Again, applying KCL, we can write:
\({\rm{i}} + \frac{{\left( {0 – {{\rm{V}}_1}} \right)}}{1} + 5 = 0 \)
i = V1 − 5 = 4 − 5 = −1 Amp
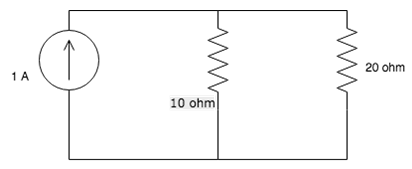
5. By using Kirchhoff’s current law calculate the current across the 20-ohm resistor.
A. 20A
Show Explanation
Answer: D
Assume a lower terminal of 20 ohms at 0V and upper terminal at V volt and applying KCL, we get
V/10 +V/20 = 1. V = 20/3V
So current through 20 ohm
= V/20 = (20/3)/20
= 1/3 = 0.33V.
6. The total charge q(t), in the coulombs, that enters the terminal of an element is:
\(q(t) = \left\{ {\begin{array}{*{20}{c}} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,t < 0}\\ {2t\,\,\,\,\,\,\,\,\,\,\,\,0 \le t \le 2}\\ {3 + {e^{ – 2(t – 2)}}\,\,t > 2} \end{array}} \right.\)
Determine the current at t = 5 s.
0 A
2 A
-2e-6 A
3 + e-6 A
Show Explanation
Answer.3.
Electric current, i = Rate of transfer of electric charge.
i(t) = dQ/dt
Calculation:
t = 5 s so, equation 3rd is consider.
\(i = \frac{{dQ}}{{dt}} = \frac{d}{{dt}}\left( {3 + {e^{ – 2\left( {t – 2} \right)}}} \right)\)
\(i = {e^{ – 2\left( {t – 2} \right)}}\frac{d}{{dt}}\left[ { – 2\left( {t – 2} \right)} \right]\)
\(i = {e^{ – 2\left( {t – 2} \right)}}\left( { – 2} \right)\)
\(i = – 2{e^{ – 2\left( {t – 2} \right)}}\)
Put the value of t = 5, then we get,
i = −2e−6 A
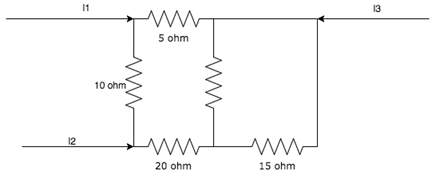
7. Calculate the value of I3, if I1 = 2A and I2 = 3A by applying Kirchhoff’s current law
A. -5A
Show Explanation
Answer: A
According to KCl, I1+I2+I3 = 0.
Hence I3 = -(I1+I2) = -5A.
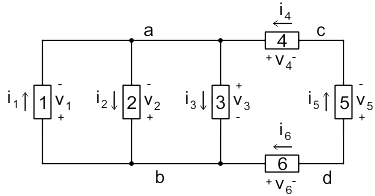
8. What would be the correct equation representing Kirchhoff’s Current Law (KCL) at node a for the given network?
i1 – i2 + i3 – i4 = 0
i1 + i2 – i3 + i4 = 0
i1 – i2 – i3 + i4 = 0
i1 – i2 = 0
Show Explanation
By applying KCL, at node a
i1 – i2 – i3 + i4 = 0
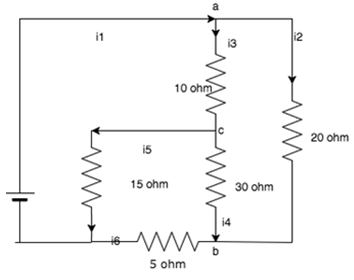
9. Find the value of i2, i4, and i5 if i1 = 3A, i3 = 1A and i6 = 1A by applying Kirchhoff’s current law
A. 2,-1,2
Show Explanation
Answer: A
At junction a: i1-i3-i2 = 0. i2 = 2A.
At junction b: i4+i2-i6 = 0. i4 = -1A.
At junction c: i3-i5-i4 = 0. i5 = 2A.
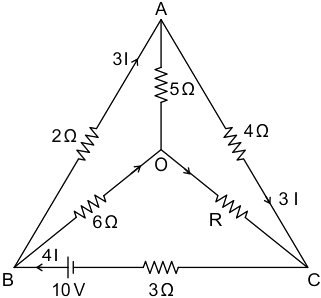
10. In the circuit shown in the following figure, calculate the value of the unknown resistance R when the current in-branch OA is zero.
5 Ω
3 Ω
12 Ω
10 Ω
Show Explanation
Answer.3. 12 Ω
Given the current through AO is zero,
It means node A and node O has the same potential,
Hence, VBA = VBO …. (1)
Also, VAC = VOC …. (2)
VAC = 4(3I) volts
VOC = IR
From equation (2),
1 × 2 I = IR
∴ R = 12 Ω