Linear Integrated Circuit MCQ [Free PDF] - Objective Question Answer for Linear Integrated Circuit Quiz

101. Find the output voltage of the log-amplifier

A. V_O = -(kT)×ln(V_i/V_ref)
B. V_O = -(kT/q)×ln(V_i/V_ref)
C. V_O = -(kT/q)×ln(V_ref/V_i)
D. V_O = (kT/q)×ln(V_i/V_ref)

Answer: B

the output voltage is proportional to the logarithm of the input voltage.

V_O =-(kT/q)×ln(V_i / V_ref).

102. How to provide saturation current and temperature compensation in log-amp?

A. Applying reference voltage alone to two different log-amps
B. Applying input and reference voltage to same log-amps
C. Applying input and reference voltage to separate log-amps
D. None of the mentioned

Answer: C

The emitter saturation current varies from transistor to transistor with temperature. Therefore, the input and reference voltage are applied to separate log-amps and two transistors are integrated close together in the same silicon wafer. This provides a close match of the saturation currents and ensures good thermal tracking.

103. The input voltage, 6v, and reference voltage, 4 v are applied to a log-amp with saturation current and temperature compensation. Find the output voltage of the log-amp?

A. 6.314(kT/q)v
B. 0.597(kT/q)v
C. 0.405(kT/q)v
D. 1.214(kT/q)v

Answer: C

The output voltage of saturation current and temperature compensation log-amp

V_O = (kT/q)×ln(V_i / V_ref)

=(kT/q)×ln(6v/4v)

=(kT/q)×ln(1.5)

V_O = 0.405(kT/q)v.

104. Determine the output voltage for the given circuit

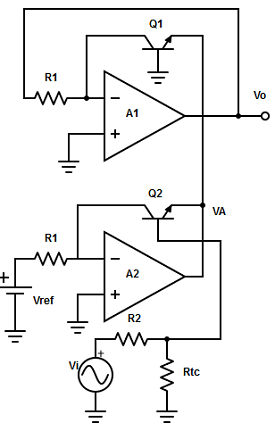
A. V_O = V_ref/(10^-k’v_i)
B. V_O = V_ref+(10^-k’v_i)
C. V_O = V_ref×(10^-k’v_i)
D. V_O = V_ref-(10^-k’v_i)

Answer: C

The output voltage of an antilog amp is given as

V_O = V_ref (10^-k’v_i)

Where k’ = 0.4343 (q/kt)×[(R_TC/ (R₂ +R_TC)].

105. Calculate the base voltage of the Q₂ transistor in the log-amp using two op-amps?

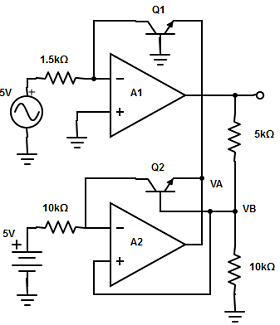
A. 8.7v
B. 5.3v
C. 3.3v
D. 6.2v

Answer: C

The base voltage of Q₂ transistor,

V_B = [R_TC / (R₂ +R_TC)]×(V_i)

= [10kΩ/(5kΩ+10kΩ)]×5v =3.33v.

106. Determine output voltage of analog multiplier provided with two input signals V_x and V_y.

A. V_o = (V_x ×V_x) / V_y
B. V_o = (V_x ×V_y / V_ref
C. V_o = (V_y ×V_y) / V_x
D. V_o = (V_x ×V_y) / V_ref²

Answer: B

The output is the product of two inputs divided by a reference voltage in the analog multiplier. Thus, the output voltage is a scaled version of x and y inputs.

=> V_o =V_x ×V_y / V_ref.

107. Match the List-I with list-II

List-I	List-II
1. One quadrant multiplier	i. Input 1- Positive, Input 2- Either positive or negative
2. Two quadrant multiplier	ii. Input 1- Positive, Input 2 – Positive
3. Four quadrant multiplier	iii. Input 1- Either positive or negative, Input 2- Either positive or negative

A. 1-ii, 2-i, 3-iii
B. 1-ii, 2-ii, 3-ii
C. 1-iii, 2-I, 3-ii
D. 1-I, 2-iii, 3-i

Answer: A

If both inputs are positive, the IC is said to be a one quadrant multiplier. A two-quadrant multiplier function properly, if one input is held positive and the other is allowed to swing. Similarly, for a four-quadrant multiplier both the inputs are allowed to swing.

108. What is the disadvantage of the log-antilog multiplier?

A. Provides four-quadrant multiplication only
B. Provides one quadrant multiplication only
C. Provides two and four-quadrant multiplication only
D. Provides one, two, and four-quadrant multiplication only

Answer: B

Log amplifier requires the input and reference voltage to be of the same polarity. This restricts the log-antilog multiplier to one quadrant operation.

109. An input of Vsinωt is applied to an ideal frequency doubler. Compute its output voltage?

A. V_o = [(V_x×V_y) /V_ref²] × [1-cos2ωt/2].
B. V_o = [(V_x²×V_y²) /V_ref] × [1-cos2ωt/2].
C. V_o = [(V_x×V_y)² /V_ref] × [1-cos2ωt/2].
D. V_o = [(V_x×V_y) /( V_ref] × [1-cos2ωt/2].

Answer: D

In an ideal frequency doubler, same frequency is applied to both inputs.

∴ V_x = V_xsinωt and V_y = V_ysinωt

=> V_o = (V_x×V_y × sin²ωt) / V_ref

= [(V_x×V_y) / V_ref] × [1-cos2ωt/2].

110. Find the output voltage for the squarer circuit given below, choose input frequency as 10kHz and V_ref =10v

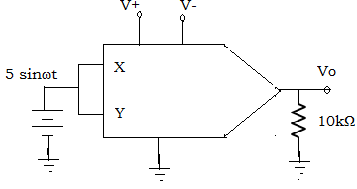
A. V_o = 5.0-(5.0×cos4π×10⁴t)
B. V_o = 2.75-(2.75×cos4π×10⁴t)
C. V_o = 1.25-(1.25×cos4π×10⁴t)
D. None of the mentioned

Answer: C

Output voltage of frequency V_o =V_i² / V_ref

=> V_i = 5sinωt = 5sin2π×10⁴t

V_o = [5×(sin2π×10⁴t)² ]/10

= 2.5×[1/2-(1/2cos2π ×2×10⁴t)] = 1.25-

(1.25×cos4π×10⁴t).

111. Calculate the phase difference between two input signals applied to a multiplier, if the input signals are V_x= 2sinωt and V_y= 4sin(ωt+θ). (Take V_ref= 12v).

A. θ = 1.019
B. θ = 30.626
C. θ = 13.87
D. θ = 45.667

Answer: A

V_o= [V_mx×V_my /(2×V_ref)] ×cosθ

=> (V_o×2×V_ref)/ (V_mx × V_my) = cosθ

=> cosθ = (10×2×12)/(2×4) = 30.

=> θ = cos^-130 =1.019.

112. Express the output voltage equation of the divider circuit

A. V_o= -(V_ref/2)×(V_z/V_x)
B. V_o= -(2×V_ref)×(V_z/V_x)
C. V_o= -(V_ref)×(V_z/V_x)
D. V_o= -V_ref²×(V_z/V_x)

Answer: C

The output voltage of the divider,

V_o= -V_ref×(V_z/V_x).

Where V_z –> dividend and V_x –> divisor.

113. Find the input current for the circuit given below.

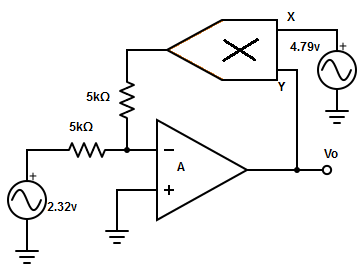
A. I_Z = 0.5372mA
B. I_Z = 1.581mA
C. I_Z = 2.436mA
D. I_Z =9.347mA

Answer: B

Input current, I_Z = -(V_x×V_o)/(V_ref×R)

= −(4.79v×16.5v)/(10×5kΩ)

= 1.581mA.

114. Find the condition at which the output will not saturate?

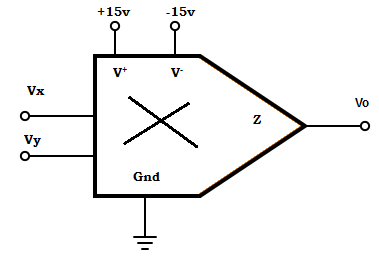
A. V_x > 10v ; V_y > 10v
B. V_x < 10v ; V_y > 10v
C. V_x < 10v ; V_y < 10v
D. V_x > 10v ; V_y < 10v

Answer: C

In an analog multiplier, V_ref is internally set to 10v. As long as V_x < V_ref and V_y < V_ref, the output of the multiplier will not saturate.

115. Determine the relationship between log-antilog method.

A. lnV_x×lnV_y = ln(V_x+V_y)
B. lnV_x / lnV_y = ln(V_x-V_y)
C. lnV_x -lnV_y = ln(V_x/V_y)
D. lnV_x+ lnV_y = ln(V_x×V_y)

Answer: D

The log-analog method relies on the mathematical relationship that is the sum of the logarithm of the product of those numbers.

=> lnV_x+lnV_y = ln(V_x×V_y).

116. Which circuit allows doubling the frequency?

A. Frequency doubler
B. Square doubler
C. Double multiplier
D. All of the mentioned

Answer: A

The multiplication of two sine waves of the same frequency with different amplitude and phases allows for doubling a frequency.

117. Compute the output of the frequency doubler. If the inputs V_x = Vsinωt and V_y = Vision(ωt+θ) are applied to a four-quadrant multiplier?

A. V_o= { V_x×V_y× [cosθ-(cosθ×cos2ωt)+(sinθ×sin2ωt)]}/ V_ref
B. V_o= { V_x×V_y× [cosθ-(cosθ×cos2ωt)+(sinθ×sin2ωt)]}/ 2
C. V_o= { V_x×V_y× [cosθ-(cosθ×cos2ωt)+(sinθ×sin2ωt)]}/(2×V_ref)
D. V_o= – { V_x×V_y× [cosθ-(cosθ×cos2ωt)+(sinθ×sin2ωt)]}/(2×V_ref)

Answer: C

The output of frequency doubler

V_o= (V_x×V_y)/V_ref = [(Vsinωt +Vsin(ωt+θ)]/ V_ref

= {V_x×V_y×[(sin²ωt×cosθ)+(sinθ×sinωt×cosωt)]}/ V_ref

=> V_o= { V_x×V_y× [cosθ-(cosθ×cos2ωt)+(sinθ×sin2ωt)]}/(2×V_ref).

118. How to remove the dc term produced along with the output in the frequency doubler?

A. Use a capacitor between load and output terminal
B. Use a resistor between load and output terminal
C. Use an Inductor between load and output terminal
D. Use a potentiometer between load and output terminal

Answer: A

The output of the frequency doubler contains a dc term and wave of double frequency. The dc term can be easily removed by using a 1µF coupling capacitor between the load and output terminal of the doubler circuit.

119. Find the voltage range at which the multiplier can be used as a squarer circuit?

A. 0 – V_in
B. V_ref – V_in
C. 0 – V_ref
D. All of the mentioned

Answer: C

The basic multiplier can be used to square any positive or negative number provided the number can be represented by a voltage between 0 to V_ref.

120. Calculate the output voltage of a squarer circuit, if its input voltage is 3.5v. Assume V_ref = 9.67v.

A. 2.86v
B. 1.27v
C. 10v
D. 4.3v

Answer: B

The output voltage of a squarer circuit

V_o = V_i² / V_ref

= (3.5)² / 9.67v = 1.27v.

Pages: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Related Posts