SOLUTION

In a P-N junction, the potential barrier is due to the charges on either side of the junction. These charges are Fixed donor and acceptor ions.

Creation of junction potential: The electric neutrality of the semiconductor material is disturbed in the region close to the junction because of the recombination which forms the depletion region. In the p-side of the depletion region, we have an accumulation of fixed negative charge ions since the atoms have acquired electrons from the n-region. Similarly, on the n-type side of the depletion region, there is an accumulation of fixed positive charge ions because the free electrons have moved to the p-region.

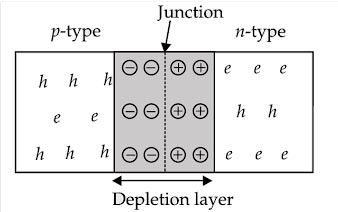
This double layer of positive and negative charges produces an electric field that exerts a force on the electrons and holes against their diffusion. The potential difference corresponding to this electric field is called the potential barrier (or junction potential or barrier potential VB). This name implies that this potential difference acts as a barrier against the diffusion of electrons and holes from their majority side to the minority side.