Rational Z Transform MCQ Quiz – Objective Question with Answer for Rational Z Transform

1. What are the values of z for which the value of X(z)=0?

A. Poles
B. Zeros
C. Solutions
D. None of the mentioned

Answer: B

For a rational z-transform X(z) to be zero, the numerator of X(z) is zero and the solutions of the numerator are called ‘zeros’ of X(z).

2. What are the values of z for which the value of X(z)=∞?

A. Poles
B. Zeros
C. Solutions
D. None of the mentioned

Answer: A

For a rational z-transform X(z) to be infinity, the denominator of X(z) is zero and the solutions of the denominator are called ‘poles’ of X(z).

3. If X(z) has M finite zeros and N finite poles, then which of the following condition is true?

A. |N-M| poles at origin(if N>M)
B. |N+M| zeros at origin(if N>M)
C. |N+M| poles at origin(if N>M)
D. |N-M| zeros at origin(if N>M)

Answer: D

If X(z) has M finite zeros and N finite poles, then X(z) can be rewritten as X(z)=z -M+N.X'(z).
So, if N>M then z has positive power. So, it has |N-M| zeros at origin.

4. If X(z) has M finite zeros and N finite poles, then which of the following condition is true?

A. |N-M| poles at origin(if N < M)
B. |N+M| zeros at origin(if N < M)
C. |N+M| poles at origin(if N < M)
D. |N-M| zeros at origin(if N < M)

Answer: A

If X(z) has M finite zeros and N finite poles, then X(z) can be rewritten as X(z)=z-M+N.X'(z).

So, if N < M then z has a negative power. So, it has |N-M| poles at the origin.

5. Which of the following signals have a pole-zero plot as shown below?

A. a.u(n)
B. u(an)
C. anu(n)
D. none of the mentioned

Answer: C

From the given pole-zero plot, the z-transform of the signal has one zero at z=0 and one pole at z=a.
So, we obtain X(z)=z/(z-A.
By applying inverse z-transform for X(z), we get
x(n)= anu(n).

6. Which of the following signals have a pole-zero plot as shown below?(Let M=8 in the figure)

A. x(n)=an, 0≤n≤8 =0, elsewhere

B. x(n)=an, 0≤n≤7 =0, elsewhere

C. x(n)=a-n, 0≤n≤8 =0, elsewhere

D. x(n)=a-n, 0≤n≤7 =0, elsewhere

Answer: B

From the figure given, the z-transform of the signal has 8 zeros on the circle of radius ‘a’ and 7 poles at the origin.
So, X(z) is of the form

X(z)=\(\frac{(z-z_1) (z-z_2)……(z-z_8)}{z^7}\)

By applying inverse z-transform, we get x(n)=an, 0≤n≤7
=0, elsewhere.

7. The z-transform X(z) of the signal x(n)=anu(n) has:

A. One pole at z=0 and one zero at z=a
B. One pole at z=0 and one zero at z=0
C. One pole at z=a and one zero at z=a
D. One pole at z=a and one zero at z=0

Answer: D

The z-transform of the given signal is X(z)=z/(z-A.
So, it has one pole at z=a and one zero at z=0.

8. What is the nature of the signal whose pole-zero plot is as shown?

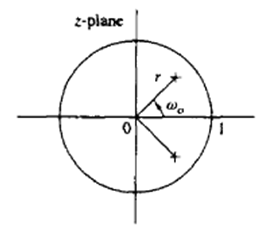
A. Rising signal
B. Constant signal
C. Decaying signal
D. None of the mentioned

Answer: C

From the pole-zero plot, it is shown that r < 1, so the signal is a decaying signal.

9. What are the values of z for which the value of X(z)=0?

A. Poles
B. Zeros
C. Solutions
D. None of the mentioned

Answer: B

For a rational z-transform X(z) to be zero, the numerator of X(z) is zero and the solutions of the numerator are called ‘zeros’ of X(z).

10. If Y(z) is the z-transform of the output function, X(z) is the z-transform of the input function and H(z) is the z-transform of the system function of the LTI system, then H(z)=?

A. \(\frac{Y(z)}{X(z)}\)

B. \(\frac{X(z)}{Y(z)}\)

C. Y(z).X(z)

D. None of the mentioned

Answer: A

We know that for an LTI system, y(n)=h(n)*x(n)
On applying z-transform on both sides we get,

Y(z)=H(z).X(z)=>H(z)=\(\frac{Y(z)}{X(z)}\)

Pages: 1 2 3

Related Posts