Ques 41. The armature current of a synchronous motor has large values for
- High excitation only
- Both low and high excitation
- Low excitation only
- None of the above
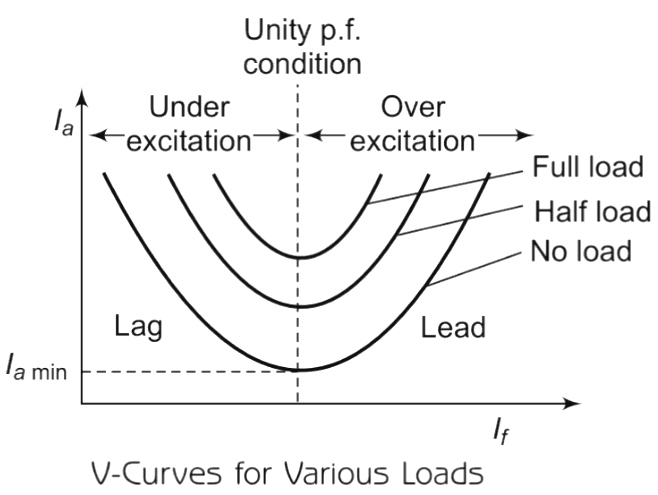
Explanation: The synchronous motor always adjusts its cosφ i.e., power factor nature so that Power component Ia cosφ remains constant when excitation of the motor is changed keeping the load constant. This is the reason why a synchronous motor reacts by changing its power factor to variable excitation conditions. Under excitation condition: When the excitation is adjusted in such a way that the magnitude of induced emf is less than the applied voltage (Eb < V) the excitation is called under excitation. Due to this, ER increases in magnitude. This means for constant Synchronous Impedance (Zs), the current drawn by the motor increases. But ER, the phase shift in such a way that, phasor Ia, also shifts (as ER ∧ Ia = θ) to keep the Power component of Ia i.e Ia cosφ components constant. So in under excited conditions, the current drawn by the motor increases. The power factor cosφ decreases and becomes more and more lagging in nature. Over excitation condition: The excitation to the field winding for which the induced emf becomes greater than the applied voltage (Eb > V) is called overexcitation. Due to the increased magnitude of Eb, ER also increases in magnitude. But the phase of ER also changes. Now (as ER ∧ Ia = θ) is constant, hence Ia also changes its phase, So φ changes. The Ia increases to keep Ia cosφ constant. The phase of ER changes so that Ia becomes leading with respect to Vph in over-excited conditions. So power factor of the motor becomes leading in nature. So overexcited synchronous motor works on leading power factor. So power factor decreases as over excitation increases but it becomes more and more leading in nature. Two important points stand out clearly from the above discussion : (i) The magnitude of armature current varies with excitation. The current has a large value both for low and high values of excitation (though it is lagging for low excitation and leading for higher excitation). In between, it has a minimum value corresponding to a certain excitation. (ii) For the same input, armature current varies over a wide range and so causes the power factor also to vary accordingly. When over-excited, motor runs with leading p.f. and with lagging p.f. when under-excited. In between, the p.f. is unity.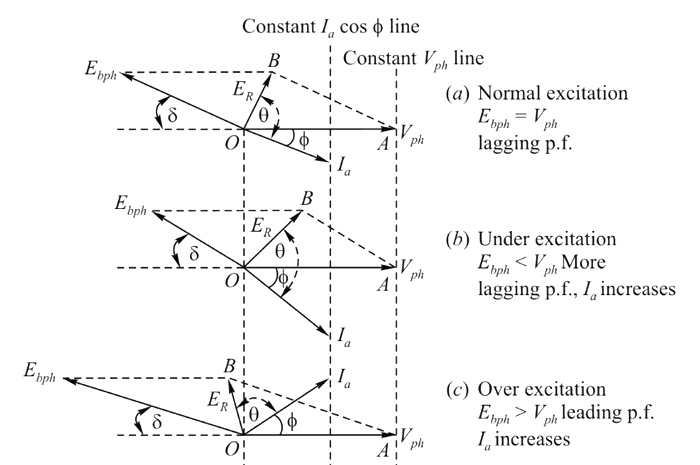
Ques 42. A synchronous motor is a useful industrial machine due to its property of
- Improving the power factor
- Speed is constant
- Can always be adjusted to operate at the unity power factor
- All of the above
Explanation: Application of Synchronous motor (a) Machine tools (b) Motor-Generator set (c) Synchronous clocks (d) Timing devices (e) Fans and blowers (f) Cement industries
Ques 43. Synchronous capacitor is
- An ordinary static capacitor bank
- An over-excited synchronous motor driving mechanical load
- An over-excited synchronous motor without mechanical load
- All of the above
Explanation: An overexcited synchronous motor acts as a power factor correction device and is also known as a synchronous condenser. The variation of armature current and power factor as a function of field current is plotted to give a better insight. In electrical engineering, a synchronous condenser(sometimes called a synchronous capacitor or synchronous compensator) is an Over-Excited Synchronous Motor, whose shaft is not connected to anything but spins freely. We can state that an over-excited synchronous motor draws a leading power factor current from the mains. The synchronous motor, therefore, when over-excited, in addition to driving some load, will work as a capacitor or condenser. A capacitor draws a leading power factor current. An over-excited synchronous motor draws the leading power factor current from the mains. An over-excited synchronous motor is also called a synchronous condenser. Synchronous motors are used as constant-speed drive motors. Over-excited synchronous motors are used to improve the power factor of electrical loads in industries. Generally, the motor is run on load, and by overexcitation, the system power factor is also improved. /bg_collapse] Ques 44. In a synchronous motor which loss does not vary with the load? Explanation: The losses in synchronous machines are as follows: (a) Fixed losses:- Core loss, bearing, friction, and windage loss, brush friction loss. These losses are obtained from the no-load test. Core loss occurs because of the eddy currents and hysteresis caused by the main magnetic field. It is the difference between the power required to drive the synchronous machine with or without field excitation. This is taken at the rated voltage and speed. (b) I2R loss in armature winding, stray loss in iron and conductors:- Armature I2R loss is current2 × dc resistance R corrected at 70°C and not the effective resistance. This can be calculated when I and R are measured. Stray load losses are caused due to changes in the flux distribution due to load. This can be found by a short-circuit test. The short-circuit current is adjusted to the value of load current at which the loss is to be determined, then the stray load loss = mechanical power input friction and windage loss I2R loss. The synchronous machine is run at the rated speed. Ventilation loss is the power required to circulate cooling air in addition to the windage loss. (c) Excitation circuit losses:- These include field copper loss, rheostat loss. brush contact loss, exciter losses. Field copper loss = I2fRf, where If is the field current and Rf is the resistance of field winding. Rheostat loss is I2fRr, where Rr, is the resistance of the rheostat. Brush contact loss is taken as slip ring current. Exciter loss is considered when it is driven by a Synchronous machine and is part of the whole machine. Otherwise, it is changed to the plant and not to the alternator. Note:- If the machine is not excited (zero field current) and running on no-load, the core loss will be zero and only windage and friction loss takes place. If the machine is excited (field current is supplied), both windage and friction and core losses take place. Thus, the core loss can be computed by taking the difference of the power consumed by machines with excitation and without excitation. It is common practice to consider core loss under load and no-load conditions the same.
Losses in Synchronous machine
Windage losses in the synchronous motor
Ques 45. A synchronous motor is said to be ‘floating‘ when it operates at
- High load and variable supply voltage
- Pulsating load
- Varying load
- No load and without losses
Explanation: Suppose that a synchronous machine is driven by a prime-mover and its stator windings are connected to a three-phase ac supply. The operation of the machine is synchronized such that no current flows through its stator windings. Under this condition, the excitation emf E in the armature windings is exactly equal to the bus-bar voltage V. The machine is neither receiving nor delivering any power to the bus bar. It is the prime-mover that supplies power to meet the losses in the machine, Under this condition, we say that the synchronous machine is floating on the bus bar. or When synchronized, the generated emf of the incoming machine is just equal to the bus-bar voltage. The synchronous machine will be just Floating on the bus bar, i.e. it will neither deliver nor receive any power. The prime mover driving the machine will be supplying the no-load losses only.Floating in Synchronous machine
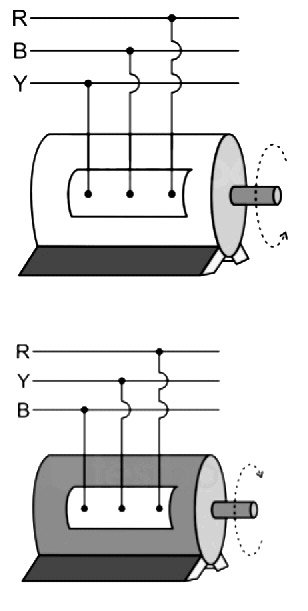
Ques 46. A 3 phase synchronous motor is running clockwise. In case the direction of its field current is reversed then
- Winding of the motor will burn
- Motor will run in the reverse direction
- Motor will continue to run in the same direction
- Motor will stop
Explanation:Reversing a Synchronous Motor
Ques 47. The rotor copper losses of the synchronous motor are met by
- Armature input
- Dc source
- Ac supply mains
- None of the above
Explanation: A synchronous machine is used to convert mechanical energy into electrical energy or vice-versa. While doing so, the whole of input energy does not appear at the output but a part of it is lost in the form of heat in the surroundings. This wasted energy is called losses in the machine. These losses affect the efficiency of the machine. The various losses occurring in a synchronous machine can be sub-divided as 1. Copper losses: The various windings of the synchronous machine such as armature and field winding are made of copper and have some resistance. When current flows through them, there will be power loss proportional to the square of their respective currents. These power losses are called copper losses. In general, the various copper losses in a synchronous machine are: (i) Armature copper loss = I2R (ii) Field winding copper loss = I2fRf (iii) Brush contact loss = I2Rb The brush contact loss is generally included in the field winding copper losses. Copper losses (both stator and field) depend on the load and they are met by a DC source. Note:-
Ques 48. If the load angle of 4 poles synchronous motor is 8o electrical its value in mechanical degree is
- 2
- 8
- 10
- 4
Explanation: Mechanical Degree: Mechanical degree or angle is the angle at which the rotor of a machine is displaced mechanically. Electrical Degree: The degree or the cycle of emf induced in a single conductor in a synchronous machine. In one electrical cycle, the electrical angle varies from 0-360 degree Electrical Degree = (No of poles/2) × Mechanical Degree 8 = (4/2) × Mechanical Degree Mechanical Degree = 4°
Ques 49. In a synchronous motor, the synchronizing power comes into action when
- Rotor speed is less than synchronous speed
- Rotor speed is more than synchronous speed
- Rotor speed is equal to synchronous speed
- Rotor speed is either less or more than synchronous speed
Explanation: $\begin{array}{l} {P_{syn}} = \frac{{V{E_f}}}{{{X_s}}}cos\delta \\ \\ P \propto \frac{1}{{{X_s}}} \end{array}$
Ques 50. The magnitude of field flux in a 3-phase synchronous motor
- Remains constant at all loads
- Varies with speed
- Varies with load
- Varies with power factor
Explanation: In short:- The magnitude of a field flux in a 3-phase synchronous machine remains constant at all loads because this motor runs at a constant speed for that The magnitude of field flux must be constant. The field is supplied from a d.c. source and the stator coils with a three-phase current.
FOR TRANSMISSION AND DISTRIBUTION SYSTEM MCQ CLICK HERE
FOR DC MOTOR MCQ CLICK HERE
FOR 1-Φ INDUCTION MOTOR MCQ CLICK HERE
FOR 3-Φ INDUCTION MOTOR MCQ CLICK HERE
FOR SYNCHRONOUS GENERATOR OR ALTERNATOR MCQ CLICK HERE
FOR SYNCHRONOUS MOTOR MCQ CLICK HERE
FOR DC MOTOR MCQ CLICK HERE
FOR DC GENERATOR MCQ CLICK HERE
FOR POWER SYSTEM MCQ CLICK HERE
FOR TRANSFORMER MCQ CLICK HERE
FOR BASIC ELECTRICAL MCQ CLICK HERE
FOR CONTROL SYSTEM MCQ CLICK HERE



