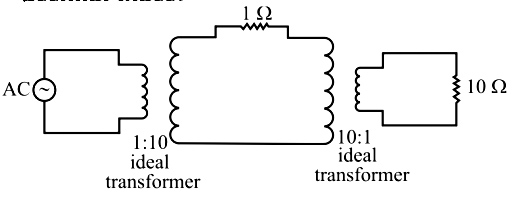
In the circuit shown, assume that the voltage source and transformers are ideal. The AC voltage source is 10√2 sin(100πt) V. The RMS value of the current flowing through the 1 Ω resistor is approximately (rounded off till first decimal place).
Right Answer is:
0.1 A
SOLUTION
Concept:
Turns ratio for the transformer is given by
$\frac{{{V_p}}}{{{V_s}}} = \frac{{{I_s}}}{{{I_p}}} = \frac{{{N_p}}}{{{N_s}}}$
Where,
Vp is voltage on primary side
Vs is voltage on secondary side
Ip is current on primary side
Is is current on secondary side
Np is turns on primary side
Ns is turns on secondary side
In transformer if R2 is the resistance connected on the secondary side.
Then the value of the secondary resistance referred to primary is $R_1’$
$\frac{{R_1′}}{{{R_2}}} = {\left( {\frac{{{N_p}}}{{{N_s}}}} \right)^2} = {\left( {\frac{{{V_p}}}{{{V_s}}}} \right)^2} = {\left( {\frac{{{I_s}}}{{{I_p}}}} \right)^2}$
Calculation:
Given that,
Voltage source is $V = 10\sqrt 2 \sin \left( {100\pi t} \right)\;V$
Referring 10Ω resistor to primary side of transformer with the transformation ratio of 10 : 1
$\frac{{R_1′}}{{10}} = {\left( {\frac{{10}}{1}} \right)^2}$
$R_1′ = 1000\;{\rm{\Omega }}$
For the transformer with 1 : 10 transformer ratio the total equivalent resistance at secondary is
$R_2′ = 1 + 1000 = 1001\;{\rm{\Omega }}$
Now referring AC voltage source $V = 10\sqrt 2 \sin \left( {100\pi t} \right)$ V to the secondary side of transformer with the transformation ratio of 1 : 10
$\frac{{10\sqrt 2 \sin \left( {100\pi t} \right)}}{{{V_s}}} = \frac{1}{{10}}$
${V_s} = 100\sqrt 2 \sin \left( {100\pi t} \right)$

RMS value of ${V_s} = 100\sqrt 2 \sin \left( {100\pi t} \right)$
Vrms = 100 V
Then the RMS value of the current flowing in the 1 Ω resistor and source RMS voltage at the secondary side is 100 V.
Therefore, the RMS value of the current flowing in the above circuit is
$I = \frac{{100}}{{1001}} = 0.099\;A \approx 0.1\;A$