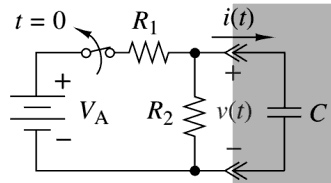
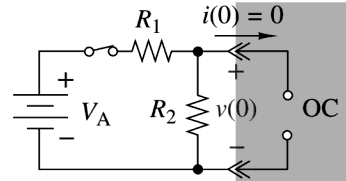
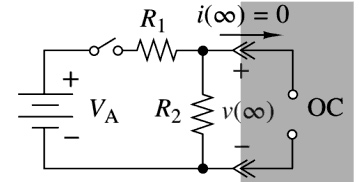
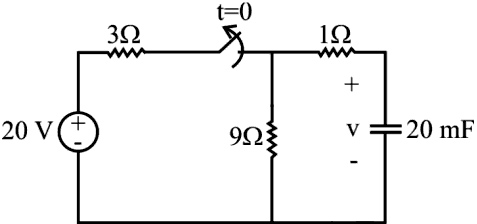
The switch in the circuit has been closed for a long time, and it is opened at time t=0. Find v(t) for t ≥ 0.
Right Answer is:
V(t) = 15e−5t V
SOLUTION
The switch in the Figure has been closed for a long time and is opened at t = 0. We want to find the capacitor voltage v(t) for t ≥ 0.
STEP 1:- The initial condition is found by dc analysis of the circuit configuration in Figure, where the switch is closed. Using the voltage division, the initial capacitor voltage is found to be
$\begin{array}{l}V(o) = \dfrac{{{R_2}{V_A}}}{{{R_1} + {R_2}}}\\\\V(o) = \dfrac{{9 \times 20}}{{9 + 3}}\end{array}$
V(o) = 15 V
STEP 2:- The final condition is found by dc analysis of the circuit configuration in Figure where the switch is open. When the switch is open the circuit has no dc excitation, so the final value of the capacitor voltage is zero.
STEP 3:- The circuit in the figure also gives us the time constant. There is an equivalent resistance of (9Ω + 1Ω), since R1 is connected in series with an open switch. For t ≥ 0 the time constant is τ. Thus the capacitor voltage for t ≥ 0 is
$V(o) = \dfrac{{{R_2}{V_A}}}{{{R_1} + {R_2}}}{e^{ – t/\tau }}$—–(1)
since, RC = τ
(9Ω + 1Ω) × 20 × 10−3
τ = 0.2 sec
Putting the value of V(o) & τ in equation 1
V(t) = 15e−t/0.2
V(t) = 15e−5t