Torque developed by a single-phase induction motor at starting is
Right Answer is:
Zero
SOLUTION
Torque developed by a single-phase induction motor at starting is Zero.
The working principle of an ac machine is primarily “one field following another field”. In the case of a multiphase induction motor, there will be a virtual rotating magnetic field. But considering the case of a single-phase induction motor, it’s only a pulsating field that is produced and not a rotating one. This can also be explained on the basis of ‘DOUBLE REVOLVING FIELD THEORY‘, which is based on Ferraris Principle
As per Ferrari’s principle, the alternating magnetic field produced by the stator can be split into two rotating magnetic fields of half the magnitude and rotating at synchronous speed in opposite directions. When the alternating supply is fed to the stator winding, an alternating flux is developed This flux rotates and cuts the rotor conductors. Due to this, an EMF is induced. As the rotor circuit is closed the current flows through the rotor conductor. This rotor current will cause rotor flux and at any instant, its magnitude is given by,
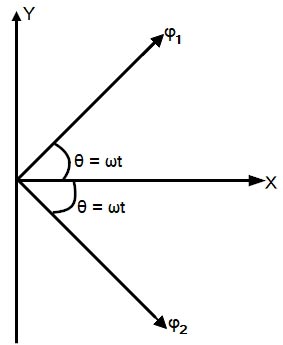
φs = φm COS ωt
where φm is the maximum flux developed in the motor. According to this theory, the alternating flux φs can be resolved into two components of and φf & φb such that the magnitude of by φf & φb is equal to half the magnitude of φs. Let us assume that φf rotates in a clockwise direction and φb rotates in the anti-clockwise direction.
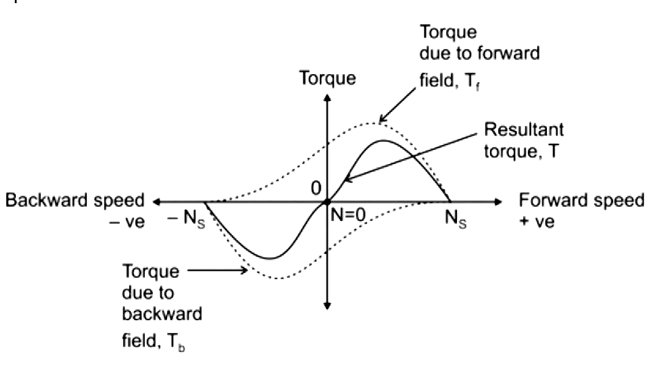
An emf is induced in the rotor circuit due to each rotating field. If the polarity of the induced emf in the rotor due to φf is taken as positive then emf induced in the rotor due to φb is negative (i.e. in phase opposition). As, at standstill, the slip in either direction is the same (i.e. s = 1), the rotor impedance will also be the same. Thus, the rotor currents are equal, but opposite in phase that is the starting torque developed by each revolving field is the same, with one acting in forward direction and the other acting in the backward direction. Thus, the net torque developed by the motor is zero.
Based on double-revolving field theory, a single-phase induction motor can be visualized as having two rotors revolving in opposite directions with a common stator winding. At standstill, the two rotors develop equal torques in opposite directions and hence the net torque developed is zero.