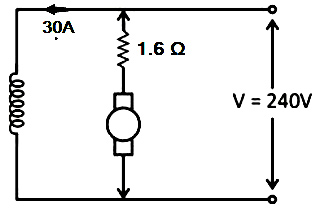
A 240 V DC shunt motor has an armature resistance of 0.6 Ω. The full load armature current is 30 A. The ratio of the stalling torque to the full load torque when the resistance of 1 Ω is connected in series with the armature is
Right Answer is:
5
SOLUTION
Stalling torque is torque at which speed falls to zero, i.e
N = 0
For DC shunt motor, speed is proportional to
$N \propto \frac{{{E_b}}}{\varphi }$
For stalling torque
Eb = V – IaRa = 0
Where,
N is the speed of the DC shunt motor
Eb is back emf
φ is flux per pole
For DC shunt motor, torque is proportional to armature current i.e. T ∝ Ia
Calculation:
Given
Total armature resistance Ra = 0.6 Ω
The full load armature current Iafull = 30 A
Terminal voltage VDC = 240 V
Now 1Ω resistance is connected in series with armature then total resistance become
Ra = 1 + 0.6 = 1.6 Ω
During Stalling torque or the breakdown torque, the speed falls to zero
Na ∝ Eb/φ
Eb = 0 & Na = 0
According to voltage equation of motor
Eb = V − IaRa
0 = 240 − 1.6 × Ia
Ia = 150 A
∵ T ∝ φIa (DC Motor)
TStalling = 150 Nm
TFull-load = 30 Nm
The ratio of stalling to full load torque is
TStalling/TFull-load = 150/30
TStalling/TFull-load = 5