Series-Parallel Grouping of Cell
The e.m.f and current which can be obtained from a single cell are generally small. The number of cells may be suitably grouped or connected together for increasing the e.m.f or current. Such a combination of cells is called a battery. Following are the three different ways of grouping the cells.
(i) Series grouping
(ii) Parallel grouping
(iii) Series parallel grouping
Cells in Series Grouping
Series Grouping When a higher terminal voltage is required, the cells are connected in series. In series, the number of cells is connected one after another, such that the negative terminal of one cell is connected to the positive terminal of the second cell and so on. Figure shows cells connected in the series grouping. Hence, in the series grouping, a group of cells can be replaced by an equivalent cell whose terminal voltage is the sum of individual terminal voltages of each cell and internal resistance is the sum of individual resistances of each cell.
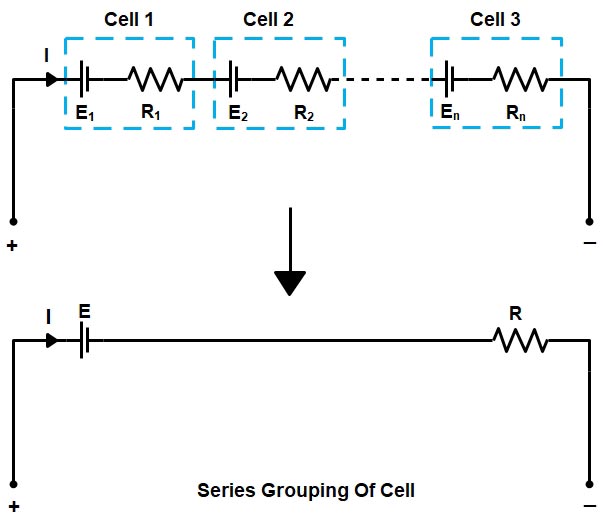
EMF of battery = Sum of E.M.F of individual cell = nE
Etotal = E1 + E2 + —– En
Cells in Parallel Grouping
Parallel Grouping When current higher than the current rating of individual cells are required, the cells are connected in parallel. In parallel grouping, the positive terminals of all the cells are connected together and brought out as the positive terminal. Similarly, the negative terminals of all the cells are connected together and brought out as the negative terminal. The figure shows cells connected in the parallel grouping. We connect cells in parallel when we want to maintain the same e.m.f. as a single cell, but wish to increase the available discharge current.
Etotal = E1 = E2 = —– En
The maximum discharge current available from cells connected in parallel is the sum of the currents deliverable by each cell.
Itotal = I1 + I2 + —– In
The total internal resistance is determined in exactly the same way as we determine the total resistance of resistors in parallel
I = 1/R1 + 1/R2 + 1/RN
Hence, in the parallel grouping, a group of cells can be replaced by an equivalent cell whose terminal voltage equals the terminal voltage of each cell and internal resistance equals the parallel combination of internal resistance of each cell.
WHEN THE CELL ARE CONNECTED IN SERIES
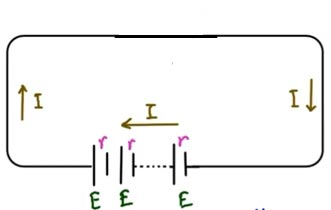
Consider the series circuit in which all the cell are connected in series. If there is “n” number of the cell than the total EMF is nE.
Now all the battery has total internal resistance therefore if n cell is connected in series that the total internal resistance will be “Rn”
Now total current in the circuit is I = nE/nR = E/R
WHEN THE CELL ARE CONNECTED IN PARALLEL
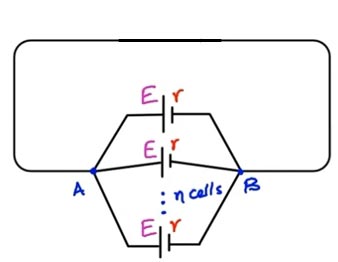
When n number of cells are connected in parallel then total EMF is equal to E (since in parallel circuit voltage remains the same).
Internal resistance in parallel = R’ = R/n
Total current in parallel circuit = I = nE/R
Now consider 3 cells each of 2V having the internal resistance of 0.1 ohm
Current in series = I = E/R = 2/0.1 = 20A
Current in parallel = I = nE/R = 60A
Hence when the individual cells are connected in parallel, the voltage is the same as that across one cell. However, the current rating of the combination equals the sum of the individual current-rating values. Only cells that have the same voltage should be connected in parallel. Whereas when the cells are connected in a series-aiding manner. The current rating of the series-aiding cells is the same as that for the cell with the lowest current rating.
Cells in Series-Parallel Combination
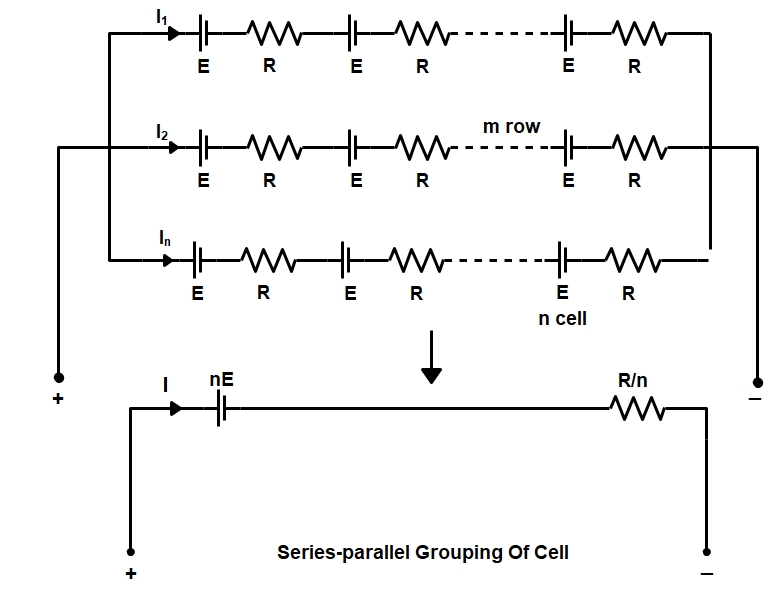
In this combination, a certain number of cells are joined in series in various rows, and all such rows are then connected in parallel with each other. Suppose n cells, each of e.m.f. E and internal resistance r, are connected in series in every row and in such rows are connected in parallel across some external resistance R, as shown in figure
If we want to increase both the terminal e.m.f. and the amount of discharge current deliverable, then a certain number of cells are joined in series in various rows, and all such rows are then connected in parallel with each other. We could connect (identical) cells in series-parallel, as illustrated in Figure.
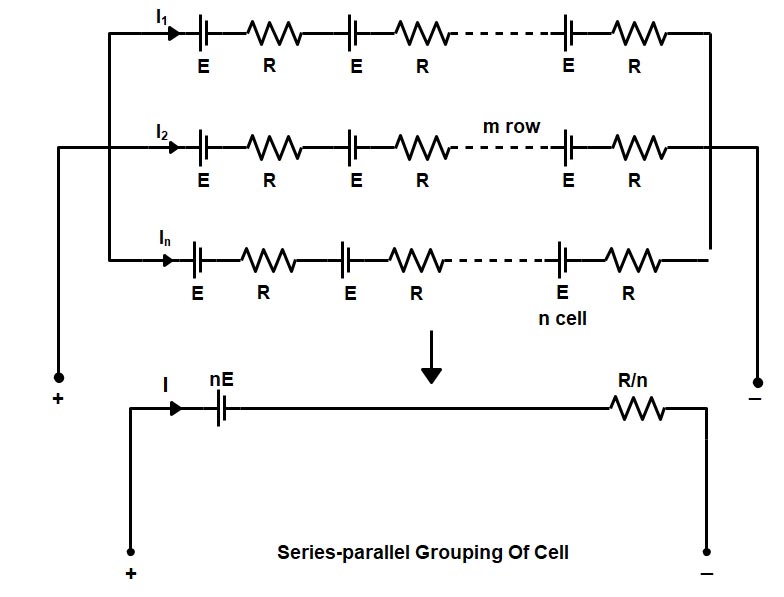
Let there be n cells connected in series in each row and m such rows connected in parallel across. As is the usual case, let all the cells be identical, each of e.m.f E volts and internal resistance of R ohms.
In the example in Figure, the total e.m.f. will be n times the e.m.f. of an individual cell i.e,
EMF of battery = EMF of one Row = nE
The total internal resistance of this arrangement can be determined in exactly the same way as we learned to determine the total resistance of any series-parallel resistive circuit.
The internal resistance of n cells in series of each row = nR
The internal resistance of battery = Equivalent resistance of m rows in parallel = nR/m
The complete battery will be capable of delivering a discharge current that is n times that of any individual branch cell (which, in turn, is that of any individual cell).
Current delivers by battery I = nE
Current delivers by whole series-parallel combination will be
I = nE/nR/m = mE/R
For Resistance In Series Parallel circuit Click Here
For Resistance In Parallel | Parallel circuit Click Here
For Resistance in series | Series Circuit Click Here
For Fundamental Of Electrical Engineering Click Here
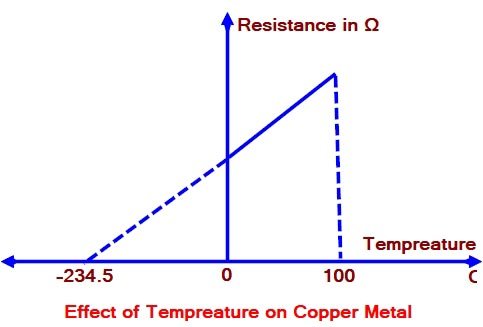
For Effect of Temperature On-Resistance Click Here
For Concept Of Resistance and Ohm’s Law Click Here
For fundamental-quantities-and-units Click Here