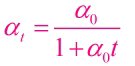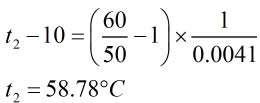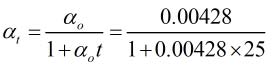Fundamental of Electrical Engineering | Effect of Temperature On Resistance| Resistance Temperature Coefficient
Effect of Temperature On Resistance
The electrical resistance changes with the change of temperature. The resistance does not only increase with the rise in temperature but it also decreases in some cases. In fact, for the different type of materials, the amount of change in resistance due to change in temperature is different which are discussed as follow.
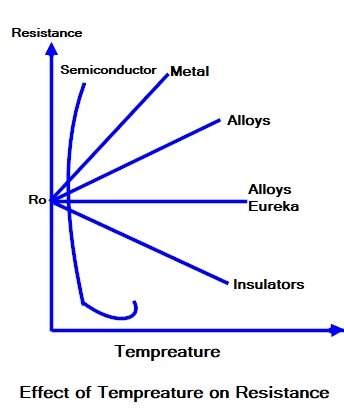
Metal: The resistance of all pure metals increases linearly with increase in temperature over a limited temperature range. At low temperature, the ions are almost stationary. As the temperature increases, the ions inside the metal acquire energy and start oscillating about their mean positions. These vibrating ions collide with the electrons Hence resistance increases with increase in temperatures.
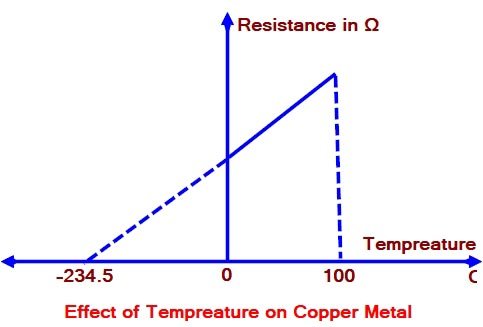
The resistance of all metals such as tungsten, copper, aluminum etc. increases linearly with increase in the temperature over a limited temperature range. For e.g. the resistance of copper is 100Ω at 0°c then it increases linearly upto 100°c. At a temperature of -234.5°c the resistance of copper is almost zero as shown in the figure.
Hence Pure metal have positive tempreature Coefficient of Resistance.
Alloy: The resistance of almost all alloys increases with increase in temperature but the rate of change of resistance is less than that of metals. In fact, the resistance of certain alloys such as Manganin, Eureka, and Constantan show practically no change in resistance fo a considerable range of temperature. Due to this property, the alloy is used to manufacture the resistance box.
Semiconductor, Insulator, and Electrolyte: The resistance of semiconductor, Insulator, and Electrolyte(silicon, Glass, Varnish etc) decrease with increase in temperature.At zero temperature, the semiconductor behaves as a perfect insulator. As the temperature increases, some of the electrons acquire energy and become free for conduction. Hence, conductivity increase and resistance decrease with increase in temperature.
Semiconductor has negative tempreature cofficent of resistivity therefore since with the increase in the tempreature the resistance decreases.
Resistance Temperature Coefficient:
The change in resistance of a material with the increase in temperature can be expressed b means of the temperature coefficient of resistance.Consider a conductor having resistance Ro at 0°c and Rt at t°c. From the above discussion, we can conclude that the change in the resistance i.e (Rt – Ro) is
- Directly proportional to the initial resistance Ro
- Directly proportional to the rise in temperature t°c.
- Depends on the nature of the material for conductor metals and alloy
Hence
(Rt – Ro) ∝ Rot
(Rt – Ro) = αRot
Rt = Ro(1 + αot)
Where αo is constant and called as the temperature coefficient of resistance at 0°c and its value depends upon the nature of material and temperature.
Effect of Temperature On Temperature Coefficient of Resistance
Let Rt1 and Rt2 be the resistance of the conductor at t1°c and t2°c respectively, and α1 and α2 be the corresponding temperature coefficient. Let the conductor is heated from initial temperature t1°c to the final temperature t2°c.
Rt2 = Rt1[1 + αt1 (t2 – t1)]——————– 1
Now the same conductor is cooled from t2°c to t1°c.
Rt1 = Rt2[1 + αt2 (t1 – t2)]———————2
Substituting equation 2 in equation 1
Rt2 = Rt2[1 + αt2 (t1 – t2)] [1 + αt1 (t2 – t1)]
Or
1 = [1 + αt2 (t1 – t2)] [1 + αt1 (t2 – t1)]
= [1 – αt2 (t2 – t1)] [1 + αt1 (t2 – t1)]
Note: If the temperature changes from 0°C to t°C then
Effect Of Temperature On Resistivity
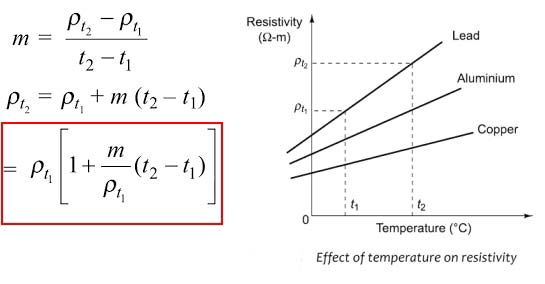
The specific resistance or resistivity of a material depends on temperature. The change in temperature affects the resistivity of a material in the same way as it affects the resistance.The resistivity of metals increases linearly with the increase in temperature. Let ρt1 and ρt2 be the resistivity at temperature t1°c and t1°c respectively. Let m be the slope of the linear part of the curve.
The ratio m/ρt1 is called the temperature coefficient of resistivity at t1°c and is almost equal to α1.
ρt2 = ρt1 [1 + αt1 (t2 – t1)]
Note: If the temperature changes from 0°C to t°C then
ρt = ρo [1 + αot]
Ques1. A piece of copper wire has a resistance of 50 Ω at 10°C. Whal is the maximum operating temperature if the resistance of the wire is to be increased by 20%? Assume α at 10°C = 0.0041°C-1.
Sol:- R1 = 50 Ω
R2 = 50 + 0.2 x 50 = 60Ω
t2 = Unkown temperature at which R2 will be 60Ω
Since
Rt2 = Rt1[1 + αt1 (t2 – t1)]
∴ R2 = R1[1 + α1 (t2 – t1)]
60 = 50[1 + 0.0041(t2 – 10)]
Ques 2. A certain winding made up of copper has a resistance of 100Ω at room temperature. if resistance temperature coefficient of copper at 0 °C is 0.00428 /°C, calculate the winding resistance temperature E increased to 50°C. Assume room temperature at 25°C.
R1 = 100 Ω
t1 = 25°C
t2 = 50°C
αo = 0.00428 /°C
Now
= 0.003866/°C
R2 = R1[1 + α1 (t2 – t1)]
R2 = 100[1 + 0.003866(50 – 25)]
=109.6657Ω