Basic Electrical | Resistance In Parallel | Parallel Circuits
Parallel Circuits
A parallel circuit is defined as one having more than one current path connected to a common voltage source. Parallel circuits, therefore, must contain two or more load resistance which is not connected in series. Each path has separate resistors (loads) and can operate independently of the other paths. The different paths for current flow are commonly called the branch of a parallel circuit.
Parallel combination of the Resistor
Two or more resistors are said to be connected in parallel if one end of a resistor is connected to one end of the other resistor and the second end of the first resistor is connected to the second end of the other resistor such that the potential difference across each resistor is the same.
One advantage of a parallel circuit is that should a break occur in one branch, it will not affect the operation of the components in the other branches, as they are still connected to the supply voltage. In a parallel circuit, the voltage is the same across every component of the circuit.
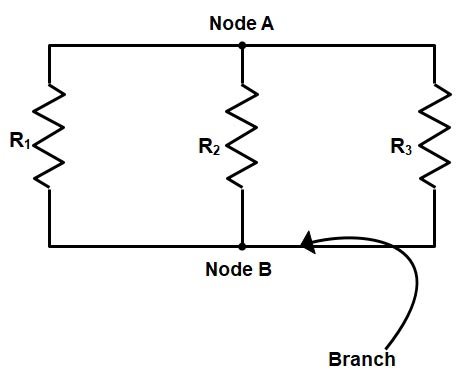
- The devices are connected in parallel when they form a loop that doesn’t encircle any other elements.
- Devices are connected in parallel when they have two nodes in common.
Equivalent Resistance of a Parallel Circuit
The combined resistance (or resultant resistance) of a number of resistances or resistors connected in parallel can be calculated by using the law of combination of resistances in parallel. According to the law of combination of resistances in parallel. The reciprocal of the combined resistance of a number of resistances connected in parallel is equal to the sum of the reciprocals of all the individual resistances. For example, if a number of resistances, R1, R2, R3, etc. are connected in parallel, then their combined resistance R is given by the formula:
1/Req = 1/R1 + 1/R2 + 1/R3
Suppose that a resistance R1 of 4 ohms R2 of 6 ohms and third resistance R3 = 12 are connected in parallel and we want to find out their combined resistance R.
We know that
1/Req = 1/4 + 1/6 + 1/12
1/Req = 6/12
Req = 2 Ω
This means that if we join three resistances of 4 ohms, 6 ohms and 12 ohms in parallel then their combined resistance is only 2 ohms which is less than either of the three individual resistances (of 4 ohms, 6 ohms, and 12 ohms). Thus, when a number of resistances are connected in parallel then their combined resistance is less than the smallest individual resistance. This is due to the fact that when we have two or more resistances joined parallel to one another, then the same current gets additional paths to flow and the overall resistance decreases.
Note:- If there are only two paths in a parallel circuit, the following formula can be used:
Req = (R1 × R2) ⁄ (R1 + R2)
The two resistances are multiplied and then added. When using this formula, it is not necessary to find the reciprocals of the resistance values. This formula may be used only when there are two resistances in a parallel circuit. If there are more than two resistances, the reciprocal formula must be used.
Another simple method of finding total resistance in a parallel circuit is when all the resistance values are the same. An example of a parallel circuit with all resistances the same is a string of lights connected in parallel. Each lamp has the same resistance. When all resistances are equal, to find total resistance, divide the resistance value of each resistor by the number of paths five 10Ω resistors are connected in parallel, the total resistance is equal to 10 divided by 5, or 2 Ω.
Voltage in Parallel Resistor Circuit
Any number of Resistors(Component) can be connected in parallel. Let us consider a parallel circuit with three Resistors, each having resistances labeled: R1, R2, and R3.
Suppose the potential difference between points A and B is V. The potential difference between any two points does not depend on the path taken between the points. The potential difference between any two points is a single fixed scalar quantity. The work done between these two points does not depend on the path taken by the test charge. A technical way of saying this is ‘the electric field is conservative’ which is also known as Kirchoff’s voltage law.
Since each resistance is connected between the same two points A and B, hence potential difference across each resistance will be the same and will be equal to applied potential difference V. Hence the voltage across all the three resistance i.e R1, R2, & R3 will be equal to the supply voltage (V).
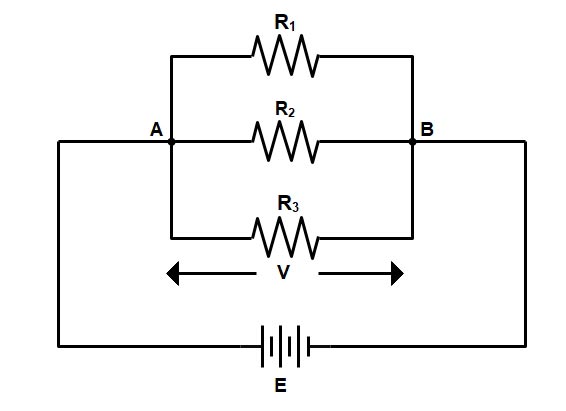
This is the major advantage of a parallel circuit and is the reason why most everyday circuits are connected in parallel. It ensures that the same voltage is applied across every component. For example, every circuit in a house is connected in parallel, ensuring that 230 V (or 120 V in North America) will appear across every component. A 230 V lamp can be connected in parallel with a 230V vacuum cleaner and a 230V electric fire, all to a 230 V supply, and they all have the same supply voltage.
Current in Parallel Resistor Circuit
If we placed ammeters into a parallel circuit, as shown in Figure, we would find that the sum of the current readings in each branch would equal the current drawn from the supply.
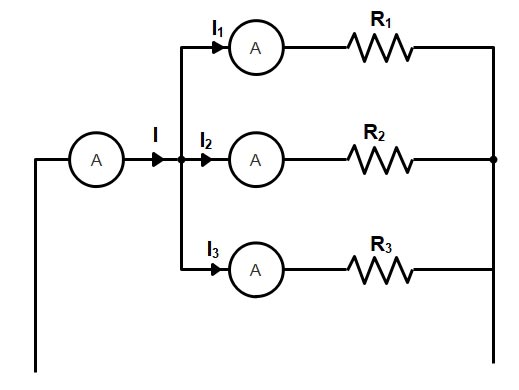
The components in a parallel circuit operate independently of one another. When two or more units are connected in parallel, each unit will receive a portion of the circuit’s total current flow. That is, the circuit’s total current divides at one or more points, and a portion travels through each resistance of the circuit. Typically, when we analyze a circuit of this type, we assume that the resistance of a wire is negligible and the power source has no internal resistance. The total current in a parallel circuit is equal to the sum of the currents in the separate components. The equation that expresses this statement follows:
IT = I1 + I2 + I3 + ——– IN
Typically, when we analyze the parallel circuit, we assume that the resistance of a wire is negligible and the power source has no internal resistance. A parallel circuit always contains more than one path for current to flow; therefore, the current can “choose” which load unit to travel through. Due to the nature of physics (and Ohm’s law), more electrons will take the path of lower and fewer electrons will take the path of higher resistance. So in a parallel circuit, any path of higher resistance naturally receives less current flow and low-resistance circuits will receive greater current flow.
From Kirchhoff’s law, the sum of the currents approaching any junction in a circuit is equal to the sum of the currents leaving the same junction, and can be expressed as follows:
I = I1 + I2 + I3
From Ohm’s Law
I = E/R
Substituting the value of I, we have
E/RT = E/R1 + E/R2 + E/R3
Since the supply voltage, E, is common to each resistance, we can divide the above equation by E:
E/RT = E/E.R1 + E/E.R2 + E/E.R3
1/RT = 1/R1 + 1/R2 + 1/R3
Where RT is the total resistance of the circuit
Summary of Parallel Circuits
- No voltage is dropped when the circuit splits into its branches; therefore, equal amounts of voltage are applied to each branch of the circuit.
- The total current in the circuit is equal to the sum of currents in its parallel branches.
- The reciprocal of the equivalent resistance is equal to the sum of the reciprocals of the individual resistances.
- The total resistance of a parallel circuit is always less than the resistance of the leg with the smallest amount of resistance.
- If one of the parallel paths is broken, current will continue to flow in all the other paths.
Advantages of Parallel Circuits in Domestic Wiring
The arrangement of lights and various other electrical appliances in parallel circuits is used in domestic wiring because of the following advantages:
- In parallel circuits, if one electrical appliance stops working due to some defect, then all other appliances keep working normally. For example, if a number of bulbs are connected in parallel circuits and one bulb gets fused (or blows out), then all the remaining bulbs will keep glowing.
- In parallel circuits, each electrical appliance has its own switch due to which it can be turned on or turned off independently, without affecting other appliances. For example, all the bulbs joined in parallel circuits in a house have separate switches due to which we can switch on or switch off any bulb as required, without affecting other bulbs in the house.
- In parallel circuits, each electrical appliance gets the same voltage (220 V) as that of the power supply line. Due to this, all the appliances will work properly. For example, all the bulbs connected in parallel circuits get the same voltage of 220 volts of the power supply line and hence glow very brightly.
- In the parallel connection of electrical appliances, the overall resistance of the household circuit is reduced due to which the current from the power supply is high. Every appliance can, therefore, draw the required amount of current. For example, in parallel circuits, even the high power rating appliances like electric irons, water heaters, and air-conditioners, etc., can draw the high current needed for their proper functioning.
Solved Example of Parallel Resistor Circuit
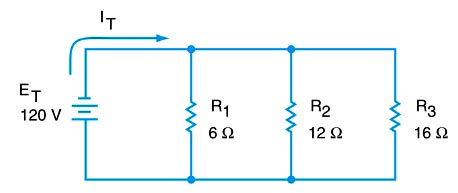
Ques.1. A circuit consists of three Resistors connected in parallel, each having a resistance of 2 Ω, 4Ω, 16Ω respectively. If the circuit is connected across a 120 V supply, calculate:
(1). The current through each branch
(2). The supply current
(3). The total resistance.
Sol:- The circuit diagram of the above question is shown in the figure
1). Current through each Branch
⇒ I1 = E/R1 = 120/6
I1 = 20 A
⇒ I2 = E/R2 = 120/12
I2 = 10 A
⇒ I3 = E/R3 = 120/16
I2 = 7.5 A
2.) The supply current
IT = I1 + I2 + I3
IT = 20 + 10 + 7.5
IT = 37.5 A
(3). The total resistance
1/Req = 1/R1 + 1/R2 + 1/R3
1/Req = 1/6 + 1/12 + 1/16
1/Req = 15/48
Req = 48/15 = 3.2 Ω
For Resistance in series | Series Circuit Click Here
For Fundamental Of Electrical Engineering Click Here
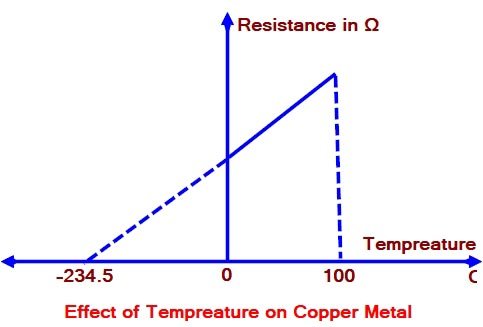
For Effect of Temperature On Resistance Click Here
For Concept Of Resistance and Ohm’s Law Click Here
For fundamental-quantities-and-units Click Here