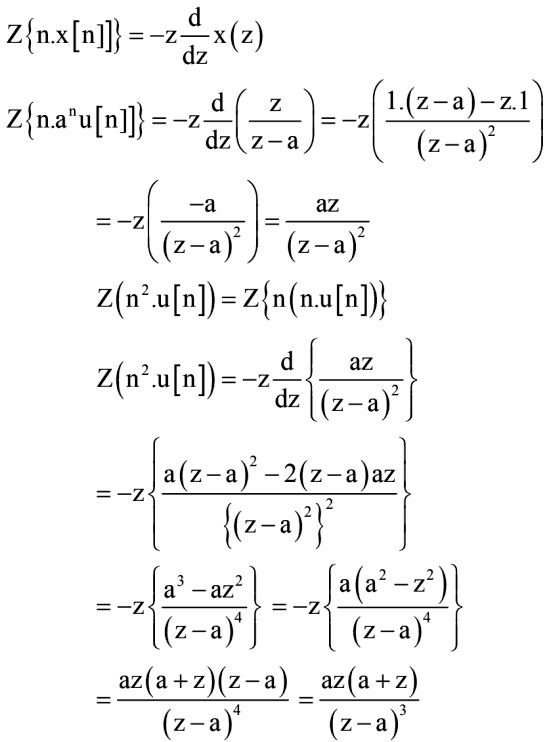A sequence u[n] is defined as $u\left[ n \right] = \left. {\left\{ \begin{array}{l}1,if{\text{ n}} \ge {\text{0}}\\1,if{\text{ n}} \le {\text{0}}\end{array} \right.{\text{ for n = \{ – }}\infty …. – 1,0,1….\infty \} } \right\}$
A sequence u[n] is defined as
$u\left[ n \right] = \left. {\left\{ \begin{array}{l}1,if{\text{ n}} \ge {\text{0}}\\1,if{\text{ n}} \le {\text{0}}\end{array} \right.{\text{ for n = \{ - }}\infty .... - 1,0,1....\infty \} } \right\}$
Consider a sequence x[n] = n2anu[n]. where a is a positive constant. The z-transform of the sequence with appropriate region of convergence is
Right Answer is:
az(z + a)/(z − a)3
SOLUTION
Given
$u\left[ n \right] = \left. {\left\{ \begin{array}{l}1,if{\text{ n}} \ge {\text{0}}\\1,if{\text{ n}} \le {\text{0}}\end{array} \right.{\text{ for n = \{ – }}\infty …. – 1,0,1….\infty \} } \right\}$
The z transform of an[n] is
$\dfrac{1}{{1 – a{z^{ – 1}}}} = \dfrac{z}{{z – a}}$
Using the multiplication by n property of z-transform i.e.