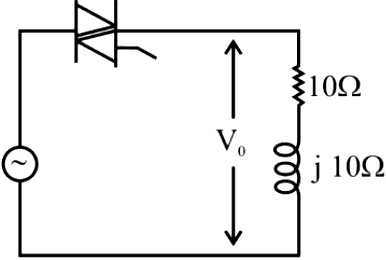
A triac based single-phase voltage regulator feeds an R-L load as shown in the figure. What is the range of triggering angle for which the output voltage Vo is not controllable?
Right Answer is:
0° ≤ α ≤ 45°
SOLUTION
Concept:
For controlling the load voltage, the minimum value of firing angle must be greater than the load phase angle.
That is, ${\alpha _{min}} > \varphi$
Where
$\varphi = {\tan ^{ – 1}}\left( {\frac{{\omega L}}{R}} \right)$
Therefore, firing angle for which the output voltage is uncontrollable is
$0 \le \alpha \le \varphi$
For controlling the load, the minimum value of firing angle α = load phase angle.
Phase angle φ = tan−1(ωL/R)
φ = tan−1(10/10) = 45°
The firing angle for which the output voltage is uncontrollable is
0 ≤ αmin ≤ φ
0° ≤ α ≤ 45°