SSC JE Electrical Conventional Paper with Explained Solution 2014 | MES Electrical
Ques 1(a):- An oven operated on a 15.0 A current from a 120 V source. How much energy will it consume in 3.0 h of operation?
Answer:- Energy consumption or power consumption refers to the electrical energy per unit time is given as
E = Power × Time = P × T
Given:-
Source Voltage = 120 V
Current = 15 A
Time = 3 hours
Power = VI
P = 120 × 15 = 1800 watts
Energy consumption in 3 Hours
= 1800 × 3 = 5400 Whr = 5.4 kWh
Ques 1(b). How many 100 W light bulbs connected to a 120 V supply can be turned on at the same time without blowing a 15.0 A fuse?
Answer:- Given
Supply voltage V = 120
Power of Bulb P = 100 W
Current I = 15 A
Now the power in an A.C circuit is given as
P = VI
P = 120 × 15 = 1800 Watts
Number of Bulbs = Power Available/Power Per Bulb
N = P/Pn = 1800/100 = 18
Hence we can illuminate 18 Bulbs at the same time without blowing 15 A fuse.
Ques 1 (c). A 120 V circuit contains 10Ω. What resistance must be added in series for the circuit to have a current of 5.0 A?
Answer:- Given
Supply Voltage V = 120 V
Resistance = 10 ohm
Require current = 5 A
Let “R” Be the unknown resistance to be added in the series then by ohms law

V = IR
120 = 5 × (10 + R)
24 = 10 + R
R = 24 − 10
R = 14 ohm
Hence 14 Ω resistance must be added in series for the circuit to have a current of 5.0 A.
Ques 1(d). In the following circuit, find the total resistance R3, V2, and I4.
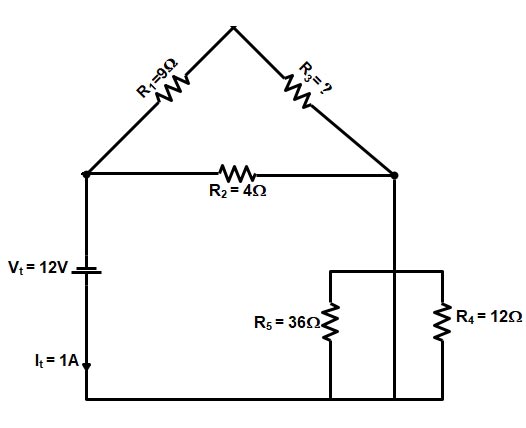
Answer:- Given
R1 = 9Ω, R2 = 4Ω
R4 = 12Ω , R5 = 36Ω
Vt = 12 V, It = 1 A
R3 = ?, V2 = ?, I4 = ?
The given circuit can be reconstructed as shown in the figure

The Resistance R1 and R3 are in series therefore equivalent Resistance is
Req1 = R1 + R3 = (9 + R3)Ω
Resistance R4 and R5 are in parallel hence equivalent resistance
Req2 = (R4 × R5)/(R4 + R5)
= (12 × 36)/(12 + 36) = 432/48 = 9Ω
After solving the resistance parameter the equivalent circuit can be reduced as shown in the figure
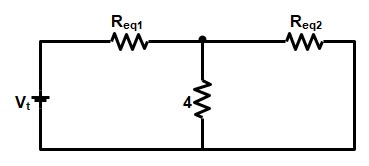
Total equvalent resistance of the circuit Req = (Req1 || 4) + Req2
Req = [(9 + R3) || 4] + 9 ——————(1)
Also Rt = Vt/It = 12/1 = 12Ω—————(2)
Equating equation 1 and 2 we get
[latex]\begin{array}{l}\dfrac{{(9 + {R_3})4}}{{13 + {R_3}}} + 9 = 12\\\\\dfrac{{36 + 4{R_3}}}{{13 + {R_3}}} = 3\\\\36 + 4{R_3} = 39 + 3{R_3}\\\\{R_3} = 3\Omega \end{array}[/latex]
⇒ Voltage across Resistance R2
Now resistance (R1 + R3) and R2 are in parallel therefore by using current divison rule
I2 = IR2
[latex]\begin{array}{l} = \dfrac{{It \times ({R_1} + {R_3})}}{{({R_1} + {R_3}) + {R_2}}}\\\\ = \dfrac{{1 \times (9 + 3)}}{{(9 + 3) + 4}}\\\\{I_2} = 0.75A\end{array}[/latex]
Hence the voltage across resistance R2
V2 = I2(R2) = 0.75 × 9 = 3V
or
V2 = Vequ = R3 × I’equ = 3 × 1 = 3V
⇒ Calculation of Current I4
Since Resistance R4 and R5 in parallel
So using current division rule
I4 = IR4
[latex]\begin{array}{l}{I_4} = \dfrac{{{I_t} \times {R_5}}}{{{R_4} + {R_5}}}\\\\ = \dfrac{{1 \times 36}}{{12 + 36}} = \dfrac{{36}}{{48}}\\\\ = 0.75A\end{array}[/latex]
So R3 = 3Ω
V2 = 3V
I4 = 0.75 A
or
V4 = Vt − V2
= 12 − 3 = 9V
I4 = V4/R4 = 9/12 = 0.75 A
Therefore
R3 = 3Ω, V2 = 3V, I4 = 0.75A

