SSC JE  Electrical Conventional Paper with Explained Solution 2016-17 | MES Electrical

 

Ques 1.  A conducting wire has a resistance of 5Ω. What is the resistance of another wire of the same material but having half the diameter and four times the length?

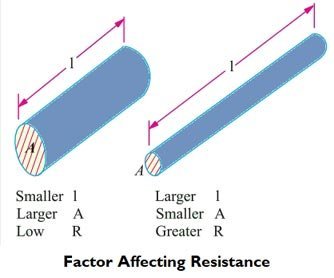
Factors Affecting the Resistance

The resistance R offered by a conductor depends on the following factors :

1. Length of the material (l): The resistance of a material is directly proportional to the length. The resistance of the longer wire is more.
2. Cross-Section Area (a): The resistance of a material is inversely proportional to the cross-sectional area of the material. More cross-sectional area allowed the passage of more number of electrons offering less resistance.
3. Nature of Material: As discussed earlier the conductor has a large number of free electrons hence it offers less resistance whereas Inductor has less number of free electrons hence it offers more resistance.
4.  
5. Temperature: The temperature of the material affects the value of the resistance. In General case, the resistance of the material increases as its temperature increases.
6.  

So for any given material at a certain given temperature, the resistance is given as

where ρ is a constant and known as its specific resistance or resistivity.
l = Length in Meter

A = area of cross-section in m²

R = Resistance in Ohm

Now suppose
Resistance of the first conductor be R₁= 5Ω
Length = L₁,
Area = A₁

Resistance of the second conductor = R₂,
Length = L₂
Area =  A₂

Given L₂ = 4L₁

A₂ = A₁/2

[latex]\begin{array}{l}{R_1} = \rho \dfrac{{{L_1}}}{{{A_1}}}\\\\{R_2} = \rho \dfrac{{{L_2}}}{{{A_2}}}\end{array}[/latex]

Dividing both the equation

[latex]\begin{array}{l}\dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{{L_2}}}{{{A_2}}} \times \dfrac{{{A_1}}}{{{L_1}}}\\\\\dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{{L_2}}}{{{L_1}}} \times \dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{L_2}}}{{{L_1}}} \times \frac{{\left( {\dfrac{{\pi {d_1}^2}}{4}} \right)}}{{\left( {\dfrac{{\pi {d_2}^2}}{4}} \right)}}\\\\\dfrac{{{R_2}}}{{{R_1}}} = \dfrac{{{L_2}}}{{{L_1}}} \times {\left( {\dfrac{{{d_1}}}{{{d_2}}}} \right)^2} = \dfrac{4}{1} \times {\left( {\dfrac{2}{1}} \right)^2}\\\\\dfrac{{{R_2}}}{5} = 16\\\\{R_2} = 80\Omega \end{array}[/latex]

 

---

Ques 2. Two coils connected in parallel across a 100V DC supply, take 10 A current from the supply. Power dissipated in one coil is 600 W. What is the resistance of each coil?

Effective Resistance of R₁ and R₂ = R₁ + R₂

Since the resistance is connected in the series therefore there effective resistance is

R_Effective = R₁R₂/(R₁ + R₂)

100V/10A = R₁R₂/(R₁ + R₂)

10Ω = R₁R₂/(R₁ + R₂)……………..(1)

Let power dissipated from resistance R1 be 600 W

Now Power P1 = V²/R₁

= 600 = 100²/R₁

or R₁ = 16.67 Ω

Putting the value of R₁ in equation 1

[latex]\begin{array}{l}10 = \dfrac{{16.67 \times {R_2}}}{{16.67 + {R_2}}}\\\\166.7 + 10{R_2} = 16.67{R_2}\\\\{R_2} = \dfrac{{166.7}}{{6.67}} = 25\Omega \end{array}[/latex]

---

Ques 3. Determine the current through 5Ω resistor in the given circuit

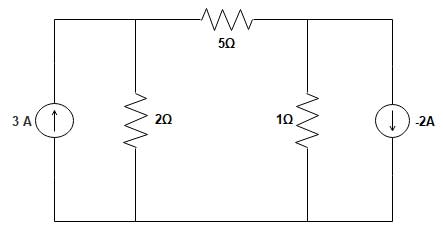
Sol:- The above circuit can be reconstructed using source transformation theorem

According to source transformation Theorem, a voltage source with a series resistor can be converted into an equivalent current source with a parallel resistor. In a similar manner, using Thevenin theorem, a current source with a parallel resistor can be represented by a voltage source with a series resistor. These transformations are called source transformations.

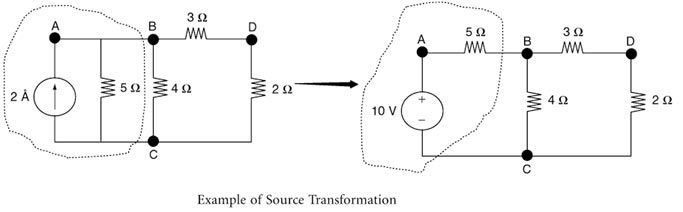
Now By applying source transformation in the above Question the given circuit will become

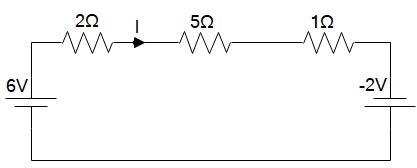
Now by applying KVL

-6 + 2I + 5I + 1I – (-2) = 0

8I = 4

I = 0.5A

---

 Ques 4.  Find the voltage across 5Ω resistance in the network shown in figure using Thevenin’s theorem

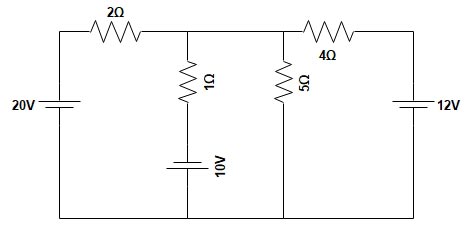
Sol:- To determine the Thevenin’s Equivalent circuit Resistance Rth, all the voltage source are replaced by the Short circuit.

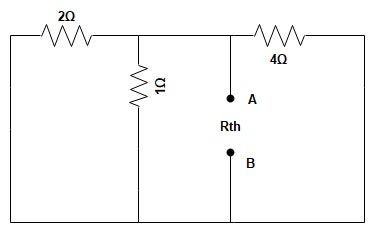
Rth = 2Ω || 1Ω || 4Ω

[latex]\begin{array}{l}{R_{th}} = \dfrac{1}{2} + \dfrac{1}{1} + \dfrac{1}{4} = \dfrac{7}{4}\\\\{R_{th}} = 0.571\Omega \end{array}[/latex]

To determine the voltage Vth the 5Ω Resitance is removed as shown in figure, Now by applying Node analysis method

[latex]\begin{array}{l}\dfrac{{{V_{th}} – 20}}{2} + \dfrac{{{V_{th}} + 10}}{1} + \dfrac{{{V_{th}} – 12}}{4} = 0\\\\2{V_{th}} – 40 + 4{V_{th}} + 40 + {V_{th}} – 12 = 0\\\\7{V_{th}} = 12\\\\{V_{th}} = 1.714V\end{array}[/latex]

The equivalent Thevnin’s circuit is shown below

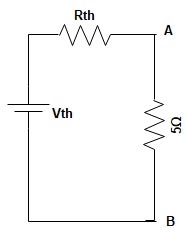
Now by applying the voltage divider rule, the voltage across the 5Ω will be

[latex]\begin{array}{l}{V_{AB}} = {V_{Th}} \times \dfrac{{{R_{th}}}}{{{R_{th}} + R}}\\\\{V_{AB}} = 1.714 \times \dfrac{5}{{5 + 0.571}}\\\\{V_{AB}} = 1.538\end{array}[/latex]

---