SSC JE Electrical Conventional Paper with Explained Solution 2015 | MES Electrical
Ques 1(a). A copper wire has a resistance of 0.85Ω at 20°C. What will be its resistance at 40°C? The temperature coefficient of resistance of copper at 0°C is 0.004°C.
Answer. Resistance Temperature Coefficient
Rt = Ro(1 + αot)
Where
Ro is the resistance at 0° Celsius
Rt is the Resistance at t° Celsius.
Given Rt = 0.85Ω at 20°C
Temperature coefficient of resistance α = 0.04°C
t = 20°
Ro = ?
0.85 = Ro [ 1 + 0.004 × 20]
0.85 = Ro×1.08
Ro = 0.787 Ω
Now the resistance of the copper at 40°C
Rt = Ro(1 + αot)
Given Rt = ? at 40°C
Temperature coefficient of resistance α = 0.04°C
t = 20°
Ro = 0.787 Ω
Rt = 0.787 [ 1 + 0.004 × 40]
[Rt = 0.912 Ω] Answer
Ques 1(b). In the circuit shown in figure what is the value of VB?

Answer:- In the above figure the two voltage sources are connected in series therefore there equivalent voltage will be (V1 + V2)
Then the total voltage in the given question will be
[V1 + (−V2)] = (6 − 5) = 1V
Veq = IR
Or IR = 1
Now potential difference across the resistor
VA − VB = IR
6 − VB = 1
∴ VB = 5V
Ques 1(c). What is the value of Thevenin voltage ETH in the given circuit as shown in the figure?
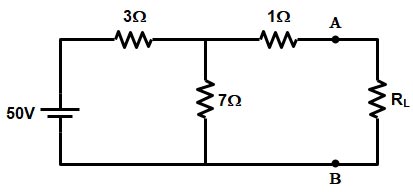
Answer:– As per Thevenin theorem, when resistance RL is connected across terminals A and B, the network behaves as a source of voltage ETh and internal resistance RT and this is called Thevenin equivalent circuit.
Thevenin Voltage
The Thevenin voltage e used in Thevenin’s Theorem is an ideal voltage source equal to the open circuit voltage at the terminals. In the given question, the resistance 1Ω does not affect this voltage and the resistances 3Ω and 7Ω form a voltage divider, giving
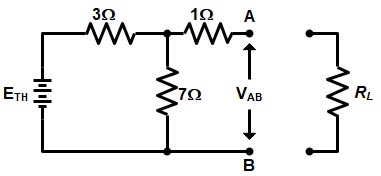
[latex]\begin{array}{l}{E_{Th}} = 50 \times \dfrac{7}{{7 + 3}}\\\\{E_{TH}} = 35V\end{array}[/latex]
Ques 1(d):- In figure find the value of resistance R
Answer:
Applying KCL at Node “1”
[latex]\dfrac{{{V_1} – 100}}{{10}} + \dfrac{{{V_1}}}{{10}} + 2 = 0[/latex]
2V1 − 100 + 20 = 0
2V1 = 80
V1 = 40 V
R = V1/I = 40/2 = 20Ω

